Full Length GRE Quantitative Reasoning Practice Test

If you want to prepare for the GRE Quantitative Reasoning Practice Test? It’s time to taking a Full-length GRE Quantitative Reasoning Practice Test. It is the best way to simulate test day. To challenge your skills and simulate the full length GRE Quantitative Reasoning Practice Test day experience, score your tests using the answer keys.

GRE Quantitative Reasoning Practice Test 1

Section 1 20 questions Total time for this section: 35 Minutes You can use a basic calculator on this section.

$a$ and $b$ are real numbers. $a<b$

Quantity A	Quantity B
$\|a\ -\ b\|$	$\|b\ -\ \| $

(A)

Quantity A is greater.

(B)

Quantity B is greater.

(C)

The two quantities are equal.

(D)

The relationship cannot be determined from the information given.

$6$ percent of $x$ is equal to $5$ percent of $y$, where $x$ and $y$ are positive numbers.

Quantity A	Quantity B
$x$	$y $

(A)

Quantity A is greater.

(B)

Quantity B is greater.

(C)

The two quantities are equal.

(D)

The relationship cannot be determined from the information given.

$x$ is an integer greater than zero.

Quantity A	Quantity B
$\frac{ 1}{x}\ +\ x $	$8 $

(A)

Quantity A is greater.

(B)

Quantity B is greater.

(C)

The two quantities are equal.

(D)

The relationship cannot be determined from the information given.

Quantity A	Quantity B
The least prime factor of $55$	The least prime factor of $210 $

(A)

Quantity A is greater.

(B)

Quantity B is greater.

(C)

The two quantities are equal.

(D)

The relationship cannot be determined from the information given.

Emma and Sophia have a family business. The profit of their business will be divided between Emma and Sophia in the ratio $3$ to $4$ respectively.;

Quantity A	Quantity B
The money Emma receives when the profit is $$560$.	The money Sophia receives when the profit is $$420$.

(A)

Quantity A is greater.

(B)

Quantity B is greater.

(C)

The two quantities are equal.

(D)

The relationship cannot be determined from the information given.

The volume of a sphere with diameter of length 5 is how many times the volume of sphere with diameter of length $\sqrt{5}$ ?
(Volume of a sphere$ =\frac{ 4}{3} \ π\ r^3)$ .

(A)

$\sqrt{5}$

(B)

${5}$

(C)

$10$

(D)

$10\sqrt{5}$

(E)

$5\sqrt{5}$

What is the solution of the following system of equations?
$\begin{cases}-\ \frac{x}{2}\ +\ \frac{y}{4}=1\\ -\ \frac{5\ y} {6}\ +\ 2\ x=4\end{cases}$

(A)

$x=48, \ y=22$

(B)

$x=50, \ y=20$

(C)

$x=20, \ y=50$

(D)

$x=22, \ y=48$

(E)

$x=22, \ y=50$

If $y=2^4$ then what is the value of $ y^\sqrt{y}$?

(A)

$2$

(B)

$2^4$

(C)

$2^8$

(D)

$2^{16}$

(E)

$2^{32}$

The average weight of $18$ girls in a class is $60$ kg and the average weight of $32$ boys in the same class is $62$ kg. What is the average weight of all the $50$ students in that class?

(A)

$60$

(B)

$61.28$

(C)

$61.68$

(D)

$61.90$

(E)

$62.20$

10-

If $60 \%$ of A is $20 \%$ of B, then B is what percent of A?

(A)

$3\%$

(B)

$30\%$

(C)

$200\%$

(D)

$300\%$

(E)

$900\%$

11-

If $(x\ -\ 2)^3=27$ which of the following could be the value of $(x\ -\ 4)\ (x\ -\ 3)$?

(A)

$1$

(B)

$2$

(C)

$6$

(D)

$-\ 1 $

(E)

$-\ 2 $

12-

The average of $ x , y$ and $5$ is $5$ and $x\ -\ y=-\ 8$ What is the value of $x\ ×\ y$ ?

(A)

$9 $

(B)

$- \ 9 $

(C)

$- \ 8 $

(D)

$ 8 $

(E)

$ 0 $

13-

The surface area of a cylinder is $150\ π$ cm$^2$. If its height is $10$ cm, what is the radius of the cylinder?

(A)

$ 13 $ cm

(B)

$ 11 $ cm

(C)

$ 15 $ cm

(D)

$ 5 $ cm

(E)

$ 7 $ cm

14-

In the $xy$-plane, the point $(4,3)$ and $(3,2)$ are on line A. Which of the following equations of lines is parallel to line A?

(A)

$ y= 3\ x$

(B)

$ y= 10$

(C)

$ y= \frac{x}{2}$

(D)

$ y=2\ x $

(E)

$ y=x $

15-

What is the product of the number of Mathematics and number of English books?
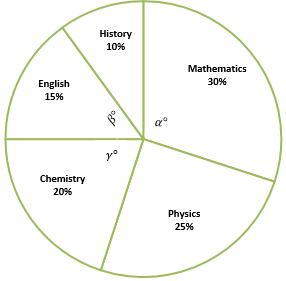GRE_Quantitative

(A)

$ 21,168 $

(B)

$ 31,752 $

(C)

$ 26,460 $

(D)

$ 17,640 $

(E)

$ 14,112 $

16-

What are the values of angle $α$ and $β$ ?
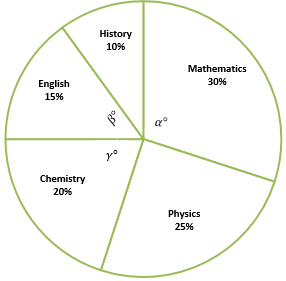GRE_Quantitative1

(A)

$ 90^ \circ , 54^\circ $

(B)

$ 120^ \circ , 36^\circ $

(C)

$ 120^ \circ , 45^\circ $

(D)

$ 108^ \circ , 54^\circ $

(E)

$ 108^ \circ , 36^\circ $

17-

The librarians decided to move some of the books in the Mathematics section to Chemistry section. How many books are in the Chemistry section if now $γ=\frac{2}{5}\ α$?
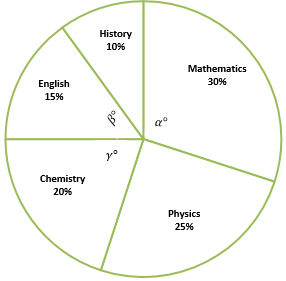GRE_Quantitative2

(A)

$80$

(B)

$120$

(C)

$150$

(D)

$180$

(E)

$200$

18-

Let $r$ and p be constants. If $x^2\ +\ 6\ x\ +\ r$ factors into $ (x \ +\ 2)\ (x \ +\ p)$, the values of $r$ and $p$ respectively are?

(A)

$8, 4 $

(B)

$4, 8 $

(C)

$6, 3 $

(D)

$3, 6 $

(E)

The answer cannot be found from the information given.

19-

In how many ways can $5$ cards be placed in $3$ positions if any cards can be placed in any position?

(A)

$5$

(B)

$10$

(C)

$15$

(D)

$30$

(E)

$120$

20-

If $(x\ -\ 2)^2\ +\ 1\ >\ 3\ x\ -\ 1$, then $x$ can equal to which of the following?

(A)

$1$

(B)

$6$

(C)

$8$

(D)

$3$

(E)

$4$

GRE Quantitative Reasoning Practice Test 1

Section 2 20 questions Total time for this section: 35 Minutes You can use a basic calculator on this section.

21-

Quantity A	Quantity B
$ (-\ 5)^4$	$ 5^4$

(A)

Quantity A is greater.

(B)

Quantity B is greater.

(C)

The two quantities are equal.

(D)

The relationship cannot be determined from the information given.

22-

The average of $3, 4$, and $x$ is $3$.

Quantity A	Quantity B
$ x$	average of $x,\ x\ -\ 6,\ x\ +\ 4,\ 2\ x$

(A)

Quantity A is greater.

(B)

Quantity B is greater.

(C)

The two quantities are equal.

(D)

The relationship cannot be determined from the information given.

23-

$\frac{4}{5}<\ x\ <\frac{6}{7}$

Quantity A	Quantity B
$ x$	$\frac{5}{6}$

(A)

Quantity A is greater.

(B)

Quantity B is greater.

(C)

The two quantities are equal.

(D)

The relationship cannot be determined from the information given.

24-

$n$ is a natural number and $\frac{1}{3^n} <\frac{1}{27}$

Quantity A	Quantity B
$ 3$	$n$

(A)

Quantity A is greater.

(B)

Quantity B is greater.

(C)

The two quantities are equal.

(D)

The relationship cannot be determined from the information given.

25-

Quantity A	Quantity B
$ \frac{ x^6}{6}$	$(\frac{x}{6})^6$

(A)

Quantity A is greater.

(B)

Quantity B is greater.

(C)

The two quantities are equal.

(D)

The relationship cannot be determined from the information given.

26-

Quantity A	Quantity B
$5\ +\ 8\ ×\ (–\ 2)\ –\ [4\ +\ 22\ ×\ 5]\ ÷\ 6 $	$[6\ ×\ (–\ 24)\ +\ 8]\ –\ (–\ 4)\ +\ [4\ ×\ 5]\ ÷\ 2 $

(A)

Quantity A is greater.

(B)

Quantity B is greater.

(C)

The two quantities are equal.

(D)

The relationship cannot be determined from the information given.

27-

If $|a|<1$, then which of the following is true? $(b>0)$?
I. $–\ b<b\ a <b$
II.$-\ a<a^2<a$ if $a<0$
III.$-\ 5<2\ a\ -\ 3<-\ 1$

(A)

I only

(B)

II only

(C)

I and III only

(D)

III only

(E)

I, II and III

28-

The ratio of boys and girls in a class is $4:7$. If there are $44$ students in the class, how many more boys should be enrolled to make the ratio $1:1$?

(A)

$8$

(B)

$10$

(C)

$12$

(D)

$14$

(E)

$28$

29-

If $150 \%$ of a number is $75$, then what is $90 \%$ of that number?

(A)

$45$

(B)

$50$

(C)

$70$

(D)

$85$

(E)

$90$

30-

Removing which of the following numbers will change the average of the numbers to $6$?
$1, \ 4, \ 5, \ 8, \ 11, \ 12$

(A)

$1$

(B)

$4$

(C)

$5$

(D)

$11$

(E)

$12$

31-

The length of a rectangle is $\frac{5}{4}$ times its width. If the width is $16$, what is the perimeter of this rectangle?

(A)

$36$

(B)

$48$

(C)

$72$

(D)

$144$

(E)

$180$

32-

The marked price of a computer is D dollar. Its price decreased by $20\%$ in January and later increased by $10 \%$ in February. What is the final price of the computer in D dollar?

(A)

$0.80$ D

(B)

$0.88$ D

(C)

$0.90$ D

(D)

$1.20$ D

(E)

$1.40$ D

33-

In the following figure, what is the perimeter of $∆ ABC$ if the area of $∆ ADC$ is $15$?
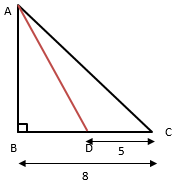GRE_Quantitative3

(A)

$37.5$

(B)

$21$

(C)

$15$

(D)

$24$

(E)

The answer cannot be determined from the information given

34-

A line $l$ is parallel to the $x$-axis and passes through the point $(-3,4)$. What is the slope of the line $(m)$ and its $y$-intercept?

(A)

$𝑚=∞, y\ −$ intercept $=4$

(B)

$𝑚=∞, y\ −$ intercept $=-\ 3$

(C)

$𝑚=0, y\ −$ intercept $=-\ 3$

(D)

$𝑚=0, y\ −$ intercept $=4$

(E)

$𝑚=-\ 3, y\ −$ intercept $=4$

35-

Between which two of the months shown was there a twenty percent decreased in the number of pants sold?
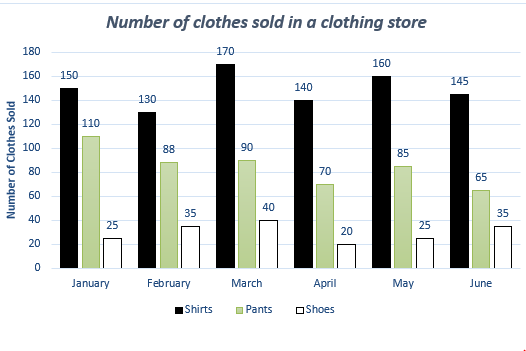GRE_Quantitative4

(A)

January and February

(B)

February and March

(C)

March and April

(D)

April and May

(E)

May and June

36-

During the six-month period shown, what is the median number of shirts and mean number of shoes per month?
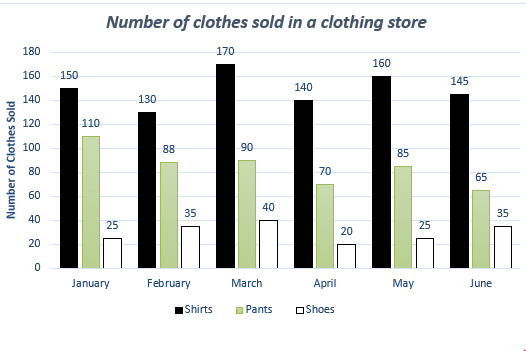GRE_Quantitative5

(A)

$146.5, 30$

(B)

$147.5, 29$

(C)

$146.5, 31$

(D)

$147.5, 30$

(E)

$146.5, 29$

37-

How many shoes need to be added in April until the ratio of number of pants to number of shoes in April equals to five-seventeenth of this ratio in May?
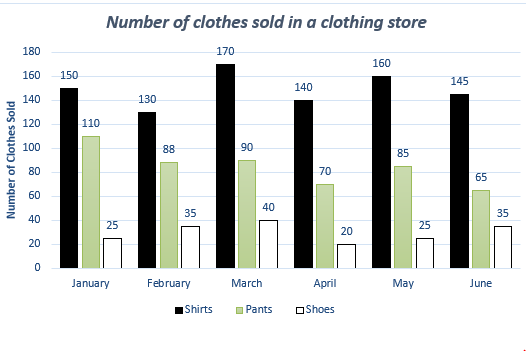GRE_Quantitative6

(A)

$90$

(B)

$80$

(C)

$70$

(D)

$60$

(E)

$50$

38-

What is the product of all possible values of $x$ in the following equation? $|x\ -\ 2\ x\ -\ 5\ +\ 7|=4$

(A)

$12$

(B)

$-\ 12$

(C)

$6$

(D)

$-\ 6$

(E)

$0$

39-

In the following figure, ABCD is a rectangle, and E and F are points on AD and DC, respectively and DE$=4$ and DF$=3$. The area of ∆BED is $16$, and the area of ∆BDF is $18$. What is the perimeter of the rectangle?
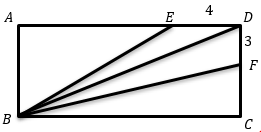GRE_Quantitative7

(A)

$20$

(B)

$22$

(C)

$32$

(D)

$40$

(E)

$44$

40-

In the following figure, ABCD is a rectangle. If a$=\sqrt{3}$, and b$=2\ a$, find the area of the shaded region. (the shaded region is a trapezoid)
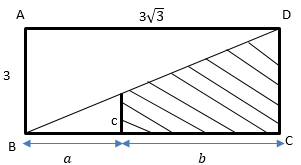GRE_Quantitative8

(A)

$4$

(B)

$2$

(C)

$\sqrt{3}$

(D)

$2\sqrt{3}$

(E)

$4\sqrt{3}$

GRE Quantitative Reasoning Practice Test Answers and Explanations

1- Choice C is correct

The correct answer is The two quantities are equal.
Choose different values for a and b and find the values of quantity A and quantity B. a$=2$ and b$=3$, then:
Quantity A: $|2\ -\ 3|=|-\ 1|=1$
Quantity B: $|3\ -\ 2|=|1|=1$ The two quantities are equal. a$=-\ 3$ and b$=2$, then:
Quantity A: $|-\ 3\ -\ 2|=|-\ 5|=5$ Quantity B: $|2\ -\ (-\ 3)|=|2\ +\ 3|=5$ The two quantities are equal. Any other values of a and b provide the same answer.

2- Choice B is correct

The correct answer is Quantity B is greater.
$6\%$ of $= 5\%$ of $y → 0.06\ x = 0.05\ y→x=\frac{0.05}{0.06} \ y→x=\frac{5}{6}\ y$, therefore, $y$ is bigger than $x$.

3- Choice D is correct

The correct answer is The relationship cannot be determined from the information given.
Choose different values for x and find the value of quantity A.
$x=1$ ,
then: Quantity A: $\frac{1}{x}\ +\ x= \frac{ 1}{1}\ +\ 1=2$
Quantity B is greater $x=0.1$, then:
Quantity A: $\frac{1}{x}\ +\ x= \frac{ 1}{0.1}\ +\ 1=10\ +\ 1=11$
Quantity A is greater
The relationship cannot be determined from the information given.

4- Choice A is correct

The correct answer is Quantity A is greater.
prime factoring of $55$ is: $5\ ×\ 11$
prime factoring of $210$ is: $2\ ×\ 3\ ×\ 5\ ×\ 7$
Quantity A $= 5$ and Quantity B $= 2$

5- Choice C is correct

The correct answer is The two quantities are equal.
The profit of their business will be divided between Emma and Sophia in the ratio $3$ to $4$ respectively.
Therefore, Emma receives $\frac{3}{7}$ of the whole profile and Sophia receives $\frac{4}{7}$ of the whole profile.
Quantity A: The money Emma receives when the profit is $$560$ equals: $\frac{3}{7}\ ×\ 560=240$
Quantity B: The money Sophia receives when the profit is $$420$ equals: $\frac{4}{7}\ ×\ 420=240$
The two quantities are equal.

6- Choice E is correct

The correct answer is $5\sqrt{5}$
$V_1=\frac{4\ π}{3}\ (\frac{5}{2})^3$
$V_2=\frac{4\ π}{3}\ (\frac{\sqrt5 }{2})^3 → \frac{ V_1}{V_2} =5\sqrt5$

7- Choice D is correct

The correct answer is $x=22, \ y=48$
$\begin{cases}-\ \frac{x}{2}\ +\ \frac{y}{4}=1\\ -\ \frac{5\ y} {6}\ +\ 2\ x=4\end{cases}$ →multiply the top equation by 4 then:
$\begin{cases} -\ 2\ x\ +\ y=4 \\ -\ \frac{5\ y}{6}\ +\ 2\ x\ =4 \end{cases}$ →add two equations
$\frac{1}{6} \ y=8→y=48$, plug in the value of y into the first euation. $→ x=22$

8- Choice D is correct

The correct answer is $2^{16}$
We know that,$\sqrt[n]{a^m }=a^{\frac{m}{n}}$ then:
$\sqrt{y}=\sqrt{2^4} =2^2=4→(2^4)^4=2^{16}$

9- Choice B is correct

The correct answer is $61.28 $
average$ = \frac{sum \ of\ terms }{number \ of\ terms}$
The sum of the weight of all girls is: $18 \ ×\ 60 = 1080$ kg
The sum of the weight of all boys is: $32 \ ×\ 62 = 1984$ kg
The sum of the weight of all students is: $1080 \ +\ 1984 = 3064$ kg
average $= \frac{3064 }{50} = 61.28$

10- Choice D is correct

The corrcet answer is $300\%$
Write the equation and solve for B: $0.60$ A $= 0.20$ B, divide both sides by $0.20$, then you will have
$\frac{0.60}{0.20}$ A = B, therefore: B $= 3$ A, and B is $3$ times of A or it’s $300\%$ of A.

11- Choice B is correct

The correct answer is $2$
$(x\ -\ 2)^3=27→x\ -\ 2=3→x=5
→(x\ -\ 4)\ (x\ -\ 3)=(5\ -\ 4)\ (5\ -\ 3)=(1)\ (2)=2$

12- Choice A is correct

The correct answer is $9$
average$=\frac{sum \ of\ terms}{number \ of\ terms} → \frac{x\ +\ y\ +\ 5}{3}=5→x\ +\ y=10$
$\begin{cases}x\ +\ y=10\\ x\ -\ y=-\ 8\end{cases}$ add both equations: $2\ x=2→x=1→y=9→x\ ×\ y=9$

13- Choice D is correct

The correct answer is $5$ cm
Formula for the Surface area of a cylinder is:
$SA=2\ π\ r^2+2\ π\ r\ h\ \to 150\ π=2\ π\ r^2\ +\ 2\ π\ r\ (10)\to r^2\ +\ 10\ r\ -\ 75=0 $
$(r\ +\ 15)\ (r\ -\ 5)=0\to r=5 $ or $ r= -\ 15$ (unacceptable)

14- Choice E is correct

The correct answer is $y = x$
The slop of line A is: $m=\frac{y_2\ -\ y_1}{x_2\ -\ x_1 }=\frac{3\ -\ 2}{4\ -\ 3}=1$
Parallel lines have the same slope and only choice E $(y=)$ has slope of $1$.

15- Choice B is correct

The correct answer is $31,752$
number of Mathematics book: $0.3\ ×\ 840=252$
number of English book: $0.15\ ×\ 840=126$
product of number of Mathematics and number of English book: $252\ ×\ 126=31,752$

16- Choice D is correct

The correct answer is $108^°,54^° $
The angle $α$ is: $0.3\ ×\ 360=108^°$
The angle $β$ is: $0.15\ ×\ 360=54^°$

17- Choice B is correct

The correct answer is $120 $
According to the chart, $50\%$ of the books are in the Mathematics and Chemistry sections.
Therefore, there are $420$ books in these two sections.
$0.50 \ ×\ 840 = 420$
$γ\ +\ α=420$, and $γ=\frac{2}{5}\ α$
Replace $γ$ by $\frac{2}{5} \ α$ in the first equation.
$γ\ +\ α=420→\frac{2}{5} α\ +\ α=420→\frac{7}{5} \ α=420→$multiply both sides by $\frac{5}{7}$
$(\frac{5}{7})\ \frac{7}{5} α=420\ ×\ (\frac{5}{7})→α=\frac{420\ ×\ 5}{7}=300$
$α=300→γ=\frac{2}{5} α→γ=\frac{2}{5}\ ×\ 300=120$
There are $120$ books in the Chemistry section.

18- Choice A is correct

The correct answer is $8 $
We have: $(x\ +\ 2)\ (x\ +\ p)=x^2\ +\ (2\ +\ p)\ x\ +\ 2\ p→2\ +\ p=6→p=4$ and $r=2\ p=8$

19- Choice B is correct

The correct answer is $10 $
This question is a combination problem. The formula for combination is:
nCr $= \frac{n!}{r!\ (n\ -\ r)!}$
This formula is for the number of possible combinations of $r$ objects from a set of $n$ objects.
Using the information in the question:
$5$C$3 = \frac{5!}{3!\ (5\ -\ 3)!}=\frac{5\ × \ 4\ ×\ 3\ ×\ 2\ ×\ 1}{3\ ×\ 2\ ×\ 1\ ×\ (2\ ×\ 1)}=10$

20- Choice C is correct

The correct answer is $8$
Plug in the value of each option in the inequality.
A.$1$ $(1\ -\ 2)^2\ +\ 1>3\ (1)\ -\ 1→2>2$ No!
B. $6$ $(6\ -\ 2)^2\ +\ 1>3\ (6)\ -\ 1→17>17$ No!
C. $8$ $(8\ -\ 2)^2\ +\ 1>3\ (8)\ -\ 1→37>23$ Bingo!
D. $3$ $(3 \ -\ 2)^2\ +\ 1 >3\ (3)\ -\ 1→2>8$ No!
C $4$ $(4\ -\ 2)^2\ +\ 1>3\ (4)\ -\ 1→5>11$ No!

20- Choice C is correct

21- Choice C is correct

The correct answer is The two quantities are equal.
Simplify both quantities.
Quantity A: $ (-\ 5)^4=(-\ 5)\ ×\ (-\ 5)\ ×\ (-\ 5)\ × \ (- \ 5)=625$
Quantity B: $5\ ×\ 5\ ×\ 5\ ×\ 5=625$
The two quantities are equal.

22- Choice C is correct

The correct answer is The two quantities are equal.
Quantity A is: $\frac{3\ +\ 4\ +\ x}{3}=3→x=2$
Quantity B is: $\frac{2\ +\ (2\ -\ 6)\ +\ (2\ +\ 4)\ +\ (2\ ×\ 2)}{4}=2$

23- Choice D is correct

The correct answer is The relationship cannot be determined from the information given.
Simply change the fractions to decimals.
$\frac{4}{5}=0.80$
$\frac{6}{7}=0.857…$
$\frac{5}{6}=0.8333…$
As you can see, $x$ lies between $0.80$ and $0.857…$ and it can be $0.81$ or $0.84$.
The first one is less than $0.833…$ and the second one is greater than $0.833…$
The relationship cannot be determined from the information given.

24- Choice B is correct

The correct answer is Quantity B is greater.
$\frac{1}{3^n} <\frac{1}{27} → 3^{-\ n}<3^{-\ 3}→-\ <-\ 3$,divide both side by$-\ 1→n>3$

25- Choice A is correct

The correct answer is Quantity A is greater.
Simplify quantity B.
Quantity B: $(\frac{x}{6})^6=\frac{x^6}{6^6}$
Since, the two quantities have the same numerator $(x^6)$ and the denominator in quantity B is bigger $(6^6>6)$, then the quantity A is greater.

26- Choice A is correct

The correct answer is Quantity A is greater.
Use PEMDAS (order of operation):
Quantity A $= 5 \ +\ 8 \ ×\ (–\ 2)\ –\ [4 \ +\ 22 \ ×\ 5] \ ÷\ 6 = 5 \ +\ 8 \ ×\ (–\ 2) \ –\ [4 \ +\ 110] \ ÷\ 6 =$
$5 \ +\ 8 \ ×\ (–\ 2) \ –\ [114] \ ÷\ 6 = 5 \ +\ (–\ 16) \ –\ 19 = 5 \ +\ (–\ 16) \ – \ 19 = –\ 11 \ –\ 19 = –\ 30$
Quantity B $= [6 \ ×\ (–\ 24) \ +\ 8] \ –\ (–\ 4)\ +\ [4 \ ×\ 5] \ ÷\ 2 = [–\ 144 \ +\ 8] \ –\ (–\ 4) \ +\ [20] \ ÷\ 2 =$
$[–\ 144 \ +\ 8] \ –\ (–\ 4) \ +\ 10 = [–\ 136] \ –\ (–\ 4) \ +\ 10 = [–\ 136] \ +\ 4 \ +\ 10 = –\ 122$
$-\ 30>-\ 122$

27- Choice C is correct

The correct answer is I and III only.
I. $|a|<1→-\ 1<a<1$
Multiply all sides by b. Since,$ b>0→-\ b<b\ a<b$
II. Since, $-\ 1<a<1$,and $a<0→-\ a>a^2>a$ (plug in $\frac{-\ 1}{2}$, and check!)
III. $-\ 1<a<1$,multiply all sides by 2,then: $-\ 2<2a<2$,subtract 3 from all sides,the:
$-\ 2\ -\ 3<2\ a\ -\ 3<2\ -\ 3→-\ 5<2\ a\ -\ 3<-\ 1$

28- Choice C is correct

The correct answer is $12$
The ratio of boy to girls is $4:7$. Therefore, there are $4$ boys out of $11$ students.
To find the answer, first divide the total number of students by $11$, then multiply the result by $4$.
$44 \ ÷\ 11 = 4 ⇒ 4 \ ×\ 4 = 16$
There are $16$ boys and $28\ (44 \ –\ 16)$ girls. So, $12$ more boys should be enrolled to make the ratio $1:1$

29- Choice A is correct

The correct answer is $45$
First, find the number.
Let $x$ be the number. Write the equation and solve for $x$.
$150 \%$ of a number is $75$, then:
$1.5\ ×\ x=75 ⇒ x=75\ ÷\ 1.5=50$
$90 \%$ of $50$ is:
$0.9 \ ×\ 50 = 45$

30- Choice D is correct

The correct answer is $11$
Check each option provided:
A. $1$ $\frac{4\ +\ 5\ +\ 8\ +\ 11\ +\ 12}{5}=\frac{40}{5}=8$
B. $4$ $\frac{1\ +\ 5\ +\ 8\ +\ 11\ +\ 12}{5}=\frac{37}{5}=7.4$
C. $5$ $\frac{1\ +\ 4\ +\ 8\ +\ 11\ +\ 12}{5}=\frac{36}{5}=7.2$
D. $11$ $\frac{1\ +\ 4\ +\ 5\ +\ 8 \ +\ 12}{5}=\frac{30}{5}=6$
E. $12$ $\frac{1\ +\ 4\ +\ 5\ +\ 8\ +\ 11}{5}=\frac{29}{5}=5.8$

31- Choice C is correct

The correct answer is $72$
length of the rectangle is:$ \frac{5}{4}\ ×\ 16=20$
perimeter of rectangle is: $2\ ×\ (20\ +\ 16)=72$

32- Choice B is correct

The correct answer is $0.88$ D
To find the discount, multiply the number by $(100\% \ –$ rate of discount).
Therefore, for the first discount we get: (D) $(100\% \ –\ 20\%) =$ (D) $(0.80) = 0.80 $ D
For increase of $10\%: (0.85 $ D) $(100\% \ +\ 10\%) = (0.85$ D) $(1.10) = 0.88$ D $= 88\% $ of D

33- Choice D is correct

The correct answer is $24$
Let $x$ be the length of AB, then:
$15=\frac{x\ ×\ 5}{2}→x=6$
The length of AC $=\sqrt{6^2\ +\ 8^2 }=\sqrt{100}=10$
The perimeter of ∆ABC$=6\ +\ 8\ +\ 10=24$

34- Choice D is correct

The correct answer is $𝑚=0, y\ −$intercept $=4$
Since line $l$ is parallel to $x$-axis, therefore the slope of $l$ is equal to $0$ and the value of $y$ is the same as the value of $y$ in the point $(-\ 3, 4)$. Therefore, $y$-intercept is $4$.

35- Choice A is correct

The correct answer is January and February
First find the number of pants sold in each month.
A. January: $110$, February: $88$, March: $90$, April: $70$, May: $85$, June: $65$
Check each option provided.
January and February,
$(\frac{110 \ - \ 88}{110}) \ × \ 100=\frac{22}{110} \ × \ 100=20\%$
B. February and March, there is an increase from February to March.
C. March and April
$(\frac{90 \ - \ 70}{90}) \ × \ 100=\frac{20}{90} \ × \ 100=22.22\%$
D. April and May: there is an increase from April to May
May and June
$(\frac{85 \ - \ 65}{85}) \ × \ 100=\frac{20}{85} \ × \ 100=23.53\%$

36- Choice D is correct

The correct answer is $147.5, 30$
Let’s order number of shirts sold per month:
$130,140,145,150,160,170$
median is: $\frac{145 \ + \ 150}{2}=147.5$
Let’s list the number of shoes sold per month:
$20,25,25,35,35,40$
mean is: $\frac{20 \ + \ 25 \ + \ 25 \ + \ 35 \ + \ 35 \ + \ 40}{6}=\frac{180}{6}=30$

37- Choice E is correct

The correct answer is $50$
Let $x$ be the number of shoes need to be added in April. Then:
$\frac{70}{20 \ + \ x}=(\frac{5}{17}) \ (\frac{85}{25}) →\frac{70}{20 \ + \ x}=\frac{425}{425}=1→$
$70=20 \ + \ x→x=50$

38- Choice B is correct

The correct answer is $-\ 12$
$|x\ -\ 2\ x\ -\ 5\ +\ 7|=4→
|-\ x\ +\ 2|=4 →-\ x\ +\ 2=4$ or$-\ x\ +\ 2=-\ 4$
$→x=-\ 2$ or $x=6$
The product of all possible values of $x = (-\ 2)\ ×\ 6=-\ 12 $

39- Choice D is correct

The correct answer is $40$
The area of ∆BED is $16$, then: $\frac{4\ ×\ AB}{2}=16→4\ ×\ AB=32→AB=8$
The area of ∆BDF is $18$, then: $\frac{3\ ×\ BC}{2}=18→3\ ×\ BC=36→BC=12$
The perimeter of the rectangle is $= 2\ ×\ (8\ +\ 12)=40$

40- Choice E is correct

The correct answer is $4\sqrt{3}$
Based on triangle similarity theorem:
$\frac{a}{a\ +\ b}=\frac{c}{3}→c=\frac{3\ a}{a\ +\ b}=\frac{3\sqrt3}{3\sqrt3}=1→$
area of shaded region is:
$(\frac{c\ +\ 3}{2})\ (b)=\frac{4}{2}\ ×\ 2\sqrt{3}=4\sqrt{3}$

More Free GRE Quantitative Reasoning Practice Test

Practice Test 1

Simulate test day with an official practice test. Then, score your test. The answers come with explanations so you can learn from your mistakes.

Start Practice Test

Practice Test 2

Simulate test day with an official practice test. Then, score your test. The answers come with explanations so you can learn from your mistakes.

Start Practice Test

Full Length GRE Quantitative Reasoning Practice Test