STAAR Math
Practice Test 1
State of Texas Assessments of Academic Readiness Grade 6 Mathematics 2019 |
| 1- |
Which expression is equivalent to \(5 \ (12 \ x \ - \ 16)\)? |
| (A) |
\(− \ 20\) |
| (B) |
\(− \ 20 \ x\) |
| (C) |
\(60 \ x \ - \ 16\) |
| (D) |
\(60 \ x \ - \ 80\) |
| 2- |
Which ordered pair describes point A that is shown below?
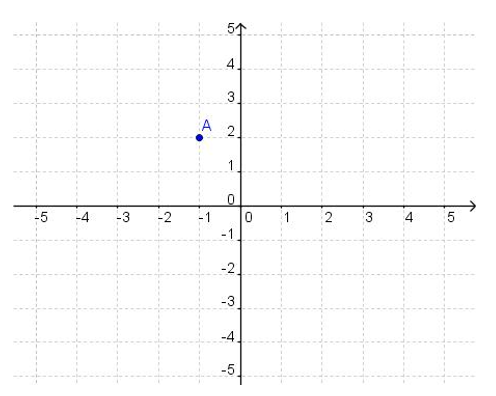 |
| (A) |
\((− \ 1,2)\) |
| (B) |
\((2,− \ 1)\) |
| (C) |
\((1, − \ 2)\) |
| (D) |
\((− \ 2,1)\) |
| 3- |
To produce a special concrete, for every \(13\) kg of cement, \(3\) liters of water is required. Which of the following ratios is the same as the ratio of cement to liters of water? |
| (A) |
\(91: 21\) |
| (B) |
\(14: 4\) |
| (C) |
\(39: 6\) |
| (D) |
\(9: 39\) |
| 4- |
Find the opposite of the numbers \(15, \ 0\). |
| (A) |
\(\frac{1}{15}, \ 0\) |
| (B) |
\(- \ 15, \ 1\) |
| (C) |
\(- \ 15, \ 0\) |
| (D) |
\(- \ \frac{1}{15}, \ 0\) |
| 5- |
What is the value of \(x\) in the following equation:
\(- \ 60=115 \ - \ x\) |
| (A) |
\(175\) |
| (B) |
\(- \ 175\) |
| (C) |
\(55\) |
| (D) |
\(- \ 55\) |
| 6- |
Which of the following graphs represents the following inequality?
\(- \ 8 \ ≤ \ 5 \ x \ - \ 8 \ ≤ \ 2\) |
| (A) |
 |
| (B) |
 |
| (C) |
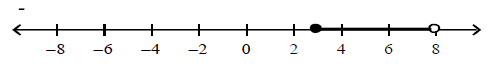 |
| (D) |
 |
| 7- |
The ratio of boys to girls in a school is \(4:5\).
If there are \(765\) students in the school, how many boys are in the school? |
| (A) |
\(612\) |
| (B) |
\(510\) |
| (C) |
\(425\) |
| (D) |
\(340\) |
| 8- |
Martin earns \($20\) an hour. Which of the following inequalities represents the amount of time Martin needs to work per day to earn at least \($100\) per day? |
| (A) |
\(20 \ t \ ≥ \ 100\) |
| (B) |
\(20 \ t \ ≤ \ 100\) |
| (C) |
\(20 \ + \ t \ ≥ \ 100\) |
| (D) |
\(20 \ + \ t \ ≤ \ 100\) |
| 9- |
\((55 \ + \ 5) \ ÷ \ 12\) is equivalent to … |
| (A) |
\(60 \ ÷ \ 3.4\) |
| (B) |
\(\frac{55}{12} \ + \ 5\) |
| (C) |
\((2 \ × \ 2 \ × \ 3 \ × \ 5) \ ÷ \ (3 \ × \ 4)\) |
| (D) |
\((2 \ × \ 2 \ × \ 3 \ × \ 5) \ ÷ \ 3 \ + \ 4\) |
| 10- |
What is the value of the expression \(6 \ (2 \ x \ - \ 3 \ y) \ + \ (3 \ - \ 2 \ x)^2\), when \(x=2\) and \(y=- \ 1\) ? |
| (A) |
\(− \ 23\) |
| (B) |
\(41\) |
| (C) |
\(43\) |
| (D) |
\(49\) |
| 11- |
Round \(\frac{215}{7}\) to the nearest tenth. |
| (A) |
\(31\) |
| (B) |
\(30.8\) |
| (C) |
\(30.7\) |
| (D) |
\(30\) |
| 12- |
A chemical solution contains \(6\%\) alcohol. If there is \(45\) ml of alcohol, what is the volume of the solution? |
| (A) |
\(270\) ml |
| (B) |
\(420\) ml |
| (C) |
\(750\) ml |
| (D) |
\(1,200\) ml |
| 13- |
What is the equation of a line that passes through points \((0, \ 4)\) and \((2, \ 8)\)? |
| (A) |
\(y = x\) |
| (B) |
\(y = x \ + \ 4\) |
| (C) |
\(y = 2 \ x \ + \ 4\) |
| (D) |
\(y = 2 \ x \ - \ 4\) |
| 14- |
What is the volume of a box with the following dimensions?
Height \(= 6\) cm Width \(= 7\) cm Length \(= 9\) cm |
| (A) |
\(63\) cm\(^3\) |
| (B) |
\(126\) cm\(^3\) |
| (C) |
\(189\) cm\(^3\) |
| (D) |
\(378\) cm\(^3\) |
| 15- |
Anita’s trick–or–treat bag contains \(14\) pieces of chocolate, \(15\) suckers, \(16\) pieces of gum, \(20\) pieces of licorice. If she randomly pulls a piece of candy from her bag, what is the probability of her pulling out a piece of sucker? |
| (A) |
\(\frac{1}{13}\) |
| (B) |
\(\frac{3}{13}\) |
| (C) |
\(\frac{14}{65}\) |
| (D) |
\(\frac{16}{65}\) |
| 16- |
In the following rectangle, which statement is false?
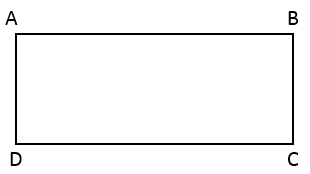 |
| (A) |
AD is parallel to BC |
| (B) |
The measure of the sum of all the angles equals \(360^°\). |
| (C) |
Length of AB equal to length DC. |
| (D) |
AB is perpendicular to AC. |
| 17- |
The area of a rectangular yard is \(90\) square meters. What is its width if its length is \(15\) meters? |
| (A) |
\(10\) meters |
| (B) |
\(8\) meters |
| (C) |
\(6\) meters |
| (D) |
\(4\) meters |
| 18- |
Which statement about \(4\) multiplied by \(\frac{3}{5}\) must be true? |
| (A) |
The product is between \(1\) and \(2\) |
| (B) |
The product is greater than \(3\) |
| (C) |
The product is equal to \(\frac{75}{31}\) |
| (D) |
The product is between \(2\) and \(2.5\) |
| 19- |
Which of the following lists shows the fractions in order from least to greatest?
\(\frac{3}{4}, \ \frac{2}{7}, \ \frac{3}{8}, \ \frac{5}{11}\) |
| (A) |
\(\frac{3}{8}, \ \frac{2}{7}, \ \frac{3}{4}, \ \frac{5}{11}\) |
| (B) |
\(\frac{2}{7}, \ \frac{5}{11}, \ \frac{3}{8}, \ \frac{3}{4}\) |
| (C) |
\(\frac{2}{7}, \ \frac{3}{8}, \ \frac{5}{11}, \ \frac{3}{4}\) |
| (D) |
\(\frac{3}{8}, \ \frac{2}{7}, \ \frac{5}{11}, \ \frac{3}{4}\) |
| 20- |
A car costing \($300\) is discounted \(10\%\). Which of the following expressions can be used to find the selling price of the car? |
| (A) |
\((300) \ (0.4)\) |
| (B) |
\(300 \ − \ (300 \ × \ 0.1)\) |
| (C) |
\((300) \ (0.1)\) |
| (D) |
\(300 \ − \ (300 \ × \ 0.9)\) |
| 21- |
What is the missing price factor of number \(420\)?
\(420=2^2 \ × \ 3^1 \ ×\)…
Write your answer in the box below. |
| (A) |
7 |
| (B) |
7 |
| (C) |
7.0 |
| 22- |
If the area of the following trapezoid is equal to A, which equation represent \(x\)?
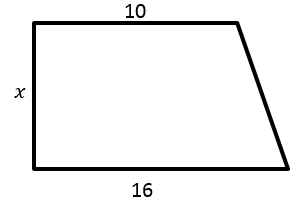 |
| (A) |
\(x = \frac{13}{A}\) |
| (B) |
\(x = \frac{A}{13}\) |
| (C) |
\(x = A \ + \ 13\) |
| (D) |
\(x = A \ - \ 13\) |
| 23- |
By what factor did the number below change from first to fourth number?
\(8, \ 104, \ 1352, \ 17576\) |
| (A) |
\(13\) |
| (B) |
\(96\) |
| (C) |
\(1456\) |
| (D) |
\(17568\) |
| 24- |
\(170\) is equal to … |
| (A) |
\(− \ 20 \ − \ (3 \ × \ 10) \ + \ (6 \ × \ 40)\) |
| (B) |
\((\frac{15}{8} \times 72) \ + \ (\frac{125}{5})\) |
| (C) |
\(((\frac{30}{4} \ + \ \frac{15}{2}) \times 8) \ - \frac{11}{2} \ + \ \frac{222}{4}\) |
| (D) |
\(\frac{481}{6} \ + \ \frac{121}{3} \ + \ 50\) |
| 25- |
The distance between two cities is \(3,768\) feet. What is the distance of the two cities in yards? |
| (A) |
\(1,256\) yd. |
| (B) |
\(11,304\) yd. |
| (C) |
\(45,216\) yd. |
| (D) |
\(3,768\) yd. |
| 26- |
Mr. Jones saves \($3,400\) out of his monthly family income of \($74,800\). What fractional part of his income does Mr. Jones save? |
| (A) |
\(\frac{1}{22}\) |
| (B) |
\(\frac{1}{11}\) |
| (C) |
\(\frac{3}{25}\) |
| (D) |
\(\frac{2}{15}\) |
| 27- |
What is the lowest common multiple of \(12\) and \(20\)? |
| (A) |
\(60\) |
| (B) |
\(40\) |
| (C) |
\(20\) |
| (D) |
\(12\) |
| 28- |
Based on the table below, which expression represents any value of \(f\) in term of its corresponding value of \(x\)?
\(x \ \ \ 3.1 \ \ 4.2 \ \ \ \ 5.9\)
\(f \ \ \ 8.6 \ \ 10.8 \ \ 14.2\) |
| (A) |
\(f = 2 \ x \ - \ \frac{3}{10}\) |
| (B) |
\(f = x \ + \ \frac{3}{10}\) |
| (C) |
\(f = 2 \ x \ + \ 2 \ \frac{2}{5}\) |
| (D) |
\(f = 2 \ x \ + \ \frac{3}{10}\) |
| 29- |
\(96\) kg … ? |
| (A) |
\(96\) mg |
| (B) |
\(9,600\) mg |
| (C) |
\(960,000\) mg |
| (D) |
\(96,000,000\) mg |
| 30- |
Calculate the approximate area of the following circle? (the diameter is \(25\))
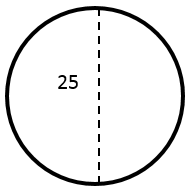 |
| (A) |
\(78\) |
| (B) |
\(491\) |
| (C) |
\(157\) |
| (D) |
\(1963\) |
| 31- |
The following graph shows the mark of six students in mathematics. What is the mean (average) of the marks?
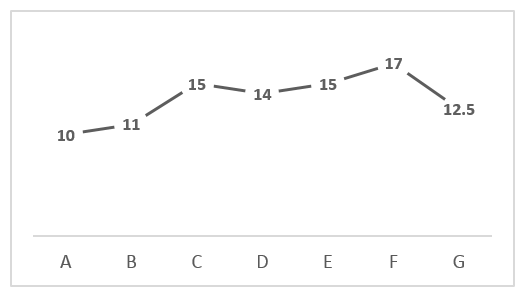 |
| (A) |
\(13\) |
| (B) |
\(13.5\) |
| (C) |
\(14\) |
| (D) |
\(15\) |
| 32- |
Which of the following statements is correct, according to the graph below?
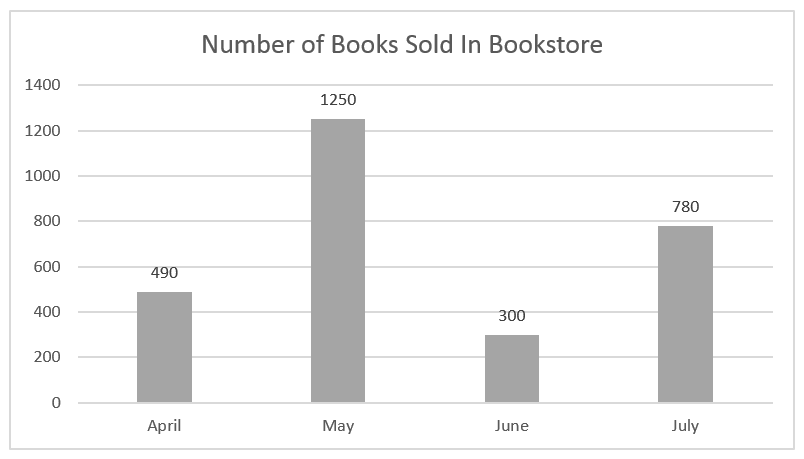 |
| (A) |
The number of books sold in the April was twice the number of books sold in the July. |
| (B) |
The number of books sold in the July was less than half the number of books sold in the May. |
| (C) |
The number of books sold in the June was more than half the number of books sold in the April. |
| (D) |
The number of books sold in the July was equal to the number of books sold in April plus the number of books sold in the June |
| 33- |
What is the ratio between α and \(β \ ( \frac{α}{β})\) in the following shape?
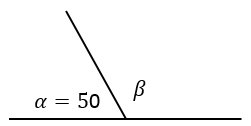 |
| (A) |
\(\frac{5}{14}\) |
| (B) |
\(\frac{5}{13}\) |
| (C) |
\(\frac{13}{5}\) |
| (D) |
\(\frac{14}{5}\) |
| 34- |
When point A \((- \ 5, \ 4)\) is reflected over the \(y-\)axis to get the point B, what are the coordinates of point B? |
| (A) |
\((− \ 5, \ − \ 4)\) |
| (B) |
\((5, \ − \ 4)\) |
| (C) |
\((5, \ 4)\) |
| (D) |
\((− \ 5, \ 4)\) |
| 35- |
In a certain bookshelf of a library, there are \(25\) biology books, \(110\) history books, and \(65\) language books. What is the ratio of the number of biology books to the total number of books in this bookshelf? |
| (A) |
\(\frac{1}{4}\) |
| (B) |
\(\frac{1}{8}\) |
| (C) |
\(\frac{2}{7}\) |
| (D) |
\(\frac{3}{8}\) |
| 36- |
Which of the following is the correct statement? |
| (A) |
\(\frac{3}{4} \ < \ 0.7\) |
| (B) |
\(25\% = \frac{1}{2} \) |
| (C) |
\(6 \ < \ \frac{12}{2} \) |
| (D) |
\(\frac{4}{5} \ > \ 0.7\) |
| 37- |
Daniel is \(66\) years old, twice as old as Henry. How old is Henry? |
| (A) |
\(23\) years’ old |
| (B) |
\(25\) years’ old |
| (C) |
\(30\) years’ old |
| (D) |
\(33\) years’ old |
| 38- |
An integer is chosen at random from \(1\) to \(30\). Find the probability of not selecting a composite number? |
| (A) |
\(\frac{13}{30}\) |
| (B) |
\(\frac{6}{15}\) |
| (C) |
\(\frac{11}{30}\) |
| (D) |
\(\frac{1}{3}\) |
| 39- |
Which of the following statements can be used for the following inequality?
\(\frac{x}{8} \ ≤ \ 16\) |
| (A) |
Sara placed \(x\) pens among \(16\) friends and each friend received fewer than \(8\) pens. |
| (B) |
Sara placed \(8\) pens among \(x\) friends and each friend received at most \(16\) pens. |
| (C) |
Sara placed \(x\) pens among \(8\) friends and each friend received fewer than \(16\) pens. |
| (D) |
Sara placed \(x\) pens among \(8\) friends and each friend received at most \(16\) pens. |
| 40- |
If the area of the following rectangular ABCD is \(140\), and E is the midpoint of AB, what is the area of the shaded part?
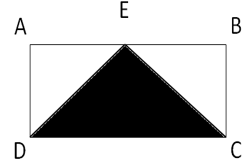 |
| (A) |
\(100\) |
| (B) |
\(70\) |
| (C) |
\(50\) |
| (D) |
\(35\) |