STAAR Math
Practice Test 2
State of Texas Assessments of Academic Readiness Grade 6 Mathematics |
| 1- |
\(4 \ (1.052) \ - \ 3.126=\)⋯? |
| (A) |
\(0.926\) |
| (B) |
\(1.082\) |
| (C) |
\(1.122\) |
| (D) |
\(1.134\) |
| 2- |
Which list shows the integer numbers listed in order from least to greatest? |
| (A) |
\(− \ 12,− \ 4,− \ 1,− \ 2,1,3,7\) |
| (B) |
\(− \ 12,− \ 1,− \ 2,− \ 4,1,3,7\) |
| (C) |
\(− \ 12,− \ 4,− \ 2,− \ 1,1,3,7\) |
| (D) |
\(− \ 1,− \ 2,− \ 4,− \ 12,1,3,7\) |
| 3- |
There are \(55\) blue marbles and \(143\) red marbles. We want to place these marbles in some boxes so that there is the same number of red marbles in each box and the same number of blue marbles in each of the boxes. How many boxes do we need? |
| (A) |
\(8\) |
| (B) |
\(9\) |
| (C) |
\(10\) |
| (D) |
\(11\) |
| 4- |
What is the value of the following expression?
\(2,205 \ ÷ \ 315\) |
| (A) |
\(5\) |
| (B) |
\(6\) |
| (C) |
\(7\) |
| (D) |
\(8\) |
| 5- |
Solve the following equation.
\(112=22 \ + \ x\) |
| (A) |
\(x=− \ 90\) |
| (B) |
\(x=90\) |
| (C) |
\(x=- \ 134\) |
| (D) |
\(x=134\) |
| 6- |
Car A travels \(221.5\) km at a given time, while car B travels \(1.2\) times the distance car A travels at the same time. What is the distance car B travels during that time? |
| (A) |
\(222.7\) km |
| (B) |
\(233.5\) km |
| (C) |
\(241.5\) km |
| (D) |
\(265.8\) km |
| 7- |
The perimeter of the trapezoid below is \(38\). What is its area?
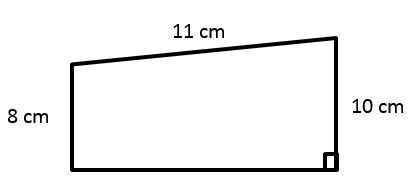 |
| (A) |
\(198\) cm\(^2\) |
| (B) |
\(162\) cm\(^2\) |
| (C) |
\(99\) cm\(^2\) |
| (D) |
\(81\) cm\(^2\) |
| 8- |
Which of the following expressions has the greatest value? |
| (A) |
\(3^1 \ + \ 12\) |
| (B) |
\(3^3 \ − \ 3^2\) |
| (C) |
\(3^4 \ − \ 60\) |
| (D) |
\(3^5 \ − \ 218\) |
| 9- |
The diameter of a circle is \(π\). What is the area of the circle? |
| (A) |
\(2 \ \pi^2\) |
| (B) |
\(\pi^2\) |
| (C) |
\(\frac{\pi^3}{3}\) |
| (D) |
\(\frac{\pi^3}{4}\) |
| 10- |
Alfred has \(x\) apples. Alvin has \(40\) apples, which is \(15\) apples less than number of apples Alfred owns. If Baron has \(\frac{1}{5}\) times as many apples as Alfred has. How many apples does Baron have? |
| (A) |
\(5\) |
| (B) |
\(11\) |
| (C) |
\(55\) |
| (D) |
\(275\) |
| 11- |
In the following triangle find \(α\).
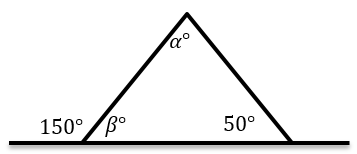 |
| (A) |
\(100^°\) |
| (B) |
\(90^°\) |
| (C) |
\(60^°\) |
| (D) |
\(30^°\) |
| 12- |
The price of a laptop is decreased by \(15\%\) to \($425\). What is its original price? |
| (A) |
\($283\) |
| (B) |
\($430\) |
| (C) |
\($500\) |
| (D) |
\($550\) |
| 13- |
Find the perimeter of shape in the following figure? (all angles are right angles)
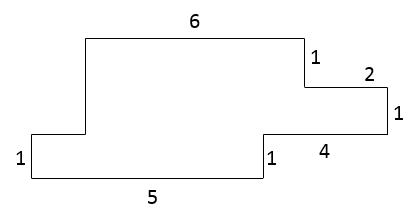 |
| (A) |
\(21\) |
| (B) |
\(22\) |
| (C) |
\(24\) |
| (D) |
\(20\) |
| 14- |
What is the probability of choosing a month starts with A in a year? |
| (A) |
\(1\) |
| (B) |
\(\frac{2}{3}\) |
| (C) |
\(\frac{1}{2}\) |
| (D) |
\(\frac{1}{6}\) |
| 15- |
What are the values of mode and median in the following set of numbers?
\(1,3,3,6,6,5,4,3,1,1,2\) |
| (A) |
Mode: \(1, \ 2,\) Median: \(2\) |
| (B) |
Mode: \(1, \ 3,\) Median: \(3\) |
| (C) |
Mode: \(2, \ 3,\) Median: \(2\) |
| (D) |
Mode: \(1, \ 3,\) Median: \(2.5\) |
| 16- |
Which expression equivalent to \(x \ × \ 92\)? |
| (A) |
\((x \ × \ 90) \ + \ 2\) |
| (B) |
\(x \ × \ 9 \ × \ 2\) |
| (C) |
\((x \ × \ 90) \ + \ (x \ × \ 2)\) |
| (D) |
\((x \ × \ 90) \ + \ 2\) |
| 17- |
The ratio of pens to pencils in a box is \(3\) to \(5\). If there are \(96\) pens and pencils in the box altogether, how many more pens should be put in the box to make the ratio of pens to pencils \(1 : 1\)? |
| (A) |
\(22\) |
| (B) |
\(23\) |
| (C) |
\(24\) |
| (D) |
\(25\) |
| 18- |
If point A placed at \(- \ \frac{24}{3}\) on a number line, which of the following points has a distance equal to \(5\) from point A? |
| (A) |
\(− \ 13\) |
| (B) |
\(− \ 3\) |
| (C) |
\(− \ 2\) |
| (D) |
A and B |
| 19- |
Which of the following shows the numbers in increasing order? |
| (A) |
\(\frac{3}{13}, \ \frac{4}{11}, \ \frac{5}{14}, \ \frac{2}{5}\) |
| (B) |
\(\frac{3}{13}, \ \frac{5}{14}, \ \frac{4}{11}, \ \frac{2}{5}\) |
| (C) |
\(\frac{3}{13}, \ \frac{5}{14}, \ \frac{2}{5}, \ \frac{4}{11}\) |
| (D) |
\(\frac{5}{14}, \ \frac{3}{13}, \ \frac{2}{5}, \ \frac{4}{11}\) |
| 20- |
If \(x= - \ 4\), which of the following equations is true? |
| (A) |
\(x \ (3 \ x \ − \ 1)=50\) |
| (B) |
\(5 \ (11 \ − \ x^2)=− \ 25\) |
| (C) |
\(3 \ (− \ 2 \ x \ + \ 5)=49\) |
| (D) |
\(x \ (− \ 5 \ x \ − \ 19)=− \ 3\) |
| 21- |
What is the missing prime factor of number \(450\)?
\(450=2^1 \ × \ 3^2 \ ×\)…
Write your answer in the box below? |
| (A) |
5 |
| (B) |
5 |
| (C) |
5.0 |
| 22- |
What is the perimeter of the following shape? (it’s a right triangle)
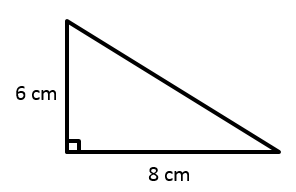 |
| (A) |
\(14\) cm |
| (B) |
\(18\) cm |
| (C) |
\(24\) cm |
| (D) |
\(32\) cm |
| 23- |
\(65\) is what percent of \(50\)? |
| (A) |
\(50\%\) |
| (B) |
\(77\%\) |
| (C) |
\(130\%\) |
| (D) |
\(140\%\) |
| 24- |
Which of the following expressions has a value of \(- \ 23\)? |
| (A) |
\(- \ 10 \ + \ ( - \ 8 ) \ + \ \frac{- \ 5}{2} \times 2\) |
| (B) |
\(5 \times 3 \ + \ ( - \ 2) \times 18\) |
| (C) |
\(− \ 10 \ + \ 6 \ × \ 8 \ ÷ \ (− \ 4)\) |
| (D) |
\((− \ 3) \ × \ (− \ 7) \ + \ 2\) |
| 25- |
\(300\) inches equal to …? |
| (A) |
\(3600\) ft. |
| (B) |
\(900\) ft. |
| (C) |
\(100\) ft. |
| (D) |
\(25\) ft. |
| 26- |
Which of the following equations is true? |
| (A) |
\(0.09= \frac{9}{100}\). |
| (B) |
\(\frac{20}{100} = 0.02\). |
| (C) |
\(2.4=\frac{24}{10}\) |
| (D) |
\(\frac{35}{7} = 0.5\) |
| 27- |
What is the greatest common factor of \(36\) and \(54\)? |
| (A) |
\(20\) |
| (B) |
\(19\) |
| (C) |
\(18\) |
| (D) |
\(17\) |
| 28- |
Based on the table below, which of the following expressions represents any value of f in term of its corresponding value of \(x\)?
\(x \ \ \ \ \ 1.1 \ \ \ \ \ 1.4 \ \ \ \ \ 2.1\)
\(f \ \ - \ 0.775 \ \ - \ 0.475 \ \ 0.225\) |
| (A) |
\(f=x \ + \ 1 \ \frac{7}{8}\) |
| (B) |
\(f=x \ - \ 1 \ \frac{7}{8}\) |
| (C) |
\(f=2 \ x \ + \ 1 \ \frac{7}{8}\) |
| (D) |
\(f=2 \ x \ - \ 1 \ \frac{7}{8}\) |
| 29- |
\(10\) mm \(=\) …? |
| (A) |
\(0.001\) m |
| (B) |
\(0.01\) m |
| (C) |
\(100\) m |
| (D) |
\(1000\) m |
| 30- |
A football team won exactly \(60\%\) of the games it played during last session. Which of the following could be the total number of games the team played last season? |
| (A) |
\(63\) |
| (B) |
\(55\) |
| (C) |
\(48\) |
| (D) |
\(37\) |
| 31- |
\(8\) less than twice a positive integer is \(70\). What is the integer? |
| (A) |
\(80\) |
| (B) |
\(78\) |
| (C) |
\(40\) |
| (D) |
\(39\) |
| 32- |
Based on the below data, what percent of cities are in the type of pollution A, C, and E respectively?
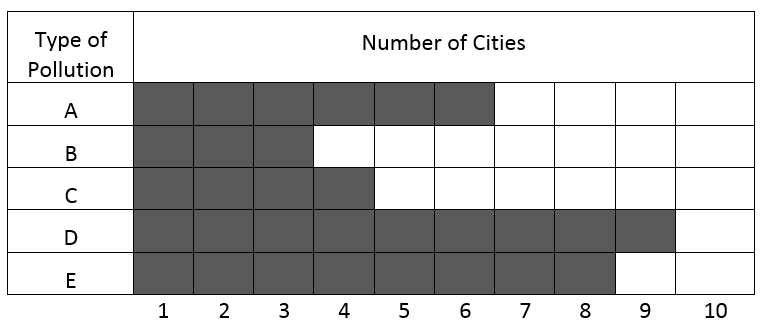 |
| (A) |
\(60\%, \ 40\%, \ 90\%\) |
| (B) |
\(30\%, \ 40\%, \ 90\%\) |
| (C) |
\(30\%, \ 40\%, \ 60\%\) |
| (D) |
\(40\%, \ 40\%, \ 90\%\) |
| 33- |
What is the missing term in the given sequence?
\(2, \ 7, \ 17, \ 37, \ 77,\) ___, \(317\)
Write your answer in the box below. |
| (A) |
157 |
| (B) |
157 |
| (C) |
157.0 |
| 34- |
If \(4 \ x \ - \ 1=9\), what is the value of \(2 \ x \ + \ 10\)? |
| (A) |
\(30.5\) |
| (B) |
\(25\) |
| (C) |
\(20.5\) |
| (D) |
\(15\) |
| 35- |
How many tiles of \(9\) cm\(^2\) is needed to cover a floor of dimension \(7\) cm by \(36\) cm? |
| (A) |
\(26\) |
| (B) |
\(27\) |
| (C) |
\(28\) |
| (D) |
\(29\) |
| 36- |
If there are \(400\) students at a school and nearly \(37\%\) of them prefer to learn Germany, approximately how many students want to learn Germany? |
| (A) |
\(400\) |
| (B) |
\(252\) |
| (C) |
\(148\) |
| (D) |
\(130\) |
| 37- |
A shaft rotates \(360\) times in \(12\) seconds. How many times does it rotate in \(18\) seconds? |
| (A) |
\(540\) |
| (B) |
\(450\) |
| (C) |
\(360\) |
| (D) |
\(100\) |
| 38- |
A card is drawn at random from a standard \(52–\)card deck, what is the probability that the card is of the soldier? |
| (A) |
\(\frac{1}{3}\) |
| (B) |
\(\frac{1}{13}\) |
| (C) |
\(\frac{1}{6}\) |
| (D) |
\(\frac{1}{52}\) |
| 39- |
Which of the following statement can describe the following inequality correctly?
\(\frac{x}{5} \ ≥ \ 9\) |
| (A) |
David put \(x\) books in \(5\) shelves, and each shelf had at least \(9\) books. |
| (B) |
David placed \(5\) books in \(x\) shelves so that each shelf had less than \(9\) books. |
| (C) |
David put \(9\) books in \(x\) shelves and each shelf had exactly \(5\) books. |
| (D) |
David put \(x\) books in \(5\) shelves, and each shelf had more than \(9\) books. |
| 40- |
Removing which of the following numbers will change the average of the numbers to \(7.4\)?
\(1, \ 4, \ 5, \ 8, \ 11, \ 12\) |
| (A) |
\(4\) |
| (B) |
\(5\) |
| (C) |
\(8\) |
| (D) |
\(11\) |