STAAR Practice Test 2
State of Texas Assessments of Academic Readiness Grade 7 Mathematics 2019 |
| 1- |
What is the slope of a line that is parallel to the line \(2 \ x \ - \ y=12\)? |
| (A) |
\(− \ 2\) |
| (B) |
\(2\) |
| (C) |
\(4\) |
| (D) |
\(12\) |
| 2- |
What is the value of the expression \(5 \ (x \ - \ 2 \ y) \ + \ (2 \ - \ x)^2\) when \(x=3\) and \(y=- \ 2\) ? |
| (A) |
\(− \ 4\) |
| (B) |
\(20\) |
| (C) |
\(36\) |
| (D) |
\(50\) |
| 3- |
The mean of \(50\) test scores was calculated as \(88\). But, it turned out that one of the scores was misread as \(94\) but it was \(69\). What is the correct mean of the data? |
| (A) |
\(85\) |
| (B) |
\(87\) |
| (C) |
\(87.5\) |
| (D) |
\(88.5\) |
| 4- |
The width of a box is one third of its length. The height of the box is one third of its width. If the length of the box is \(27\) cm, what is the volume of the box? |
| (A) |
\(81\) cm\(^3\) |
| (B) |
\(162\) cm\(^3\) |
| (C) |
\(243\) cm\(^3\) |
| (D) |
\(729\) cm\(^3\) |
| 5- |
In five successive hours, a car travels \(40\) km, \(45\) km, \(50\) km, \(35\) km and \(55\) km. In the next five hours, it travels with an average speed of \(50\) km per hour. Find the total distance the car traveled in \(10\) hours. |
| (A) |
\(425\) km |
| (B) |
\(450\) km |
| (C) |
\(475\) km |
| (D) |
\(500\) km |
| 6- |
The ratio of boys to girls in a school is \(2:3\). If there are \(600\) students in a school, how many boys are in the school.
Write your answer in the box below. |
| (A) |
240 |
| (B) |
240 |
| (C) |
240.0 |
| 7- |
The perimeter of the trapezoid below is \(54\) cm. What is its area?
Write your answer in the box below.
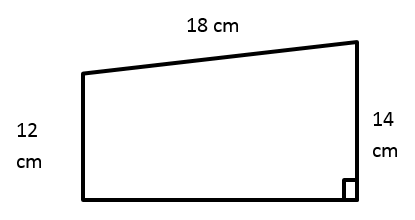 |
| (A) |
130 |
| (B) |
130 |
| (C) |
130.0 |
| 8- |
In \(1999\), the average worker's income increased \($2,000\) per year starting from \($24,000\) annual salary. Which equation represents income greater than average? (I \(=\) income, \(x =\) number of years after 1999) |
| (A) |
\(I > \ 2000 \ x \ + \ 24000\) |
| (B) |
\(I \ > \ - \ 2000 \ x \ + \ 24000\) |
| (C) |
\(I \ < \ - \ 2000 \ x \ + \ 24000\) |
| (D) |
\(I \ < \ 2000 \ x \ - \ 24000\) |
| 9- |
Which of the following graphs represents the compound inequality? |
| (A) |
 |
| (B) |
 |
| (C) |
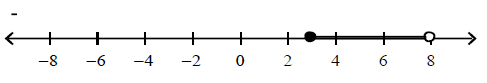 |
| (D) |
 |
| 10- |
A football team had \($20,000\) to spend on supplies. The team spent \($14,000\) on new balls. New sport shoes cost \($120\) each. Which of the following inequalities represent how many new shoes the team can purchase? |
| (A) |
\(120 \ x \ + \ 14,000 \ ≤ \ 20,000\) |
| (B) |
\(120 \ x \ + \ 14,000 \ ≥ \ 20,000\) |
| (C) |
\(14,000 \ x \ + \ 12,0 \ ≤ \ 20,000\) |
| (D) |
\(14,000 \ x \ + \ 12,0 \ ≥ \ 20,000\) |
| 11- |
Two dice are thrown simultaneously, what is the probability of getting a sum of \(6\) or \(9\)? |
| (A) |
\(\frac{1}{3}\) |
| (B) |
\(\frac{1}{4}\) |
| (C) |
\(\frac{1}{6}\) |
| (D) |
\(\frac{1}{12}\) |
| 12- |
A swimming pool holds \(2,000\) cubic feet of water. The swimming pool is \(25\) feet long and \(10\) feet wide. How deep is the swimming pool?
Write your answer in the box below. |
| (A) |
8 |
| (B) |
8 |
| (C) |
8.0 |
| 13- |
Which graph corresponds to the following inequalities?
\(y \leq x \ + \ 4\)
\(2 \ x \ + \ y \leq - \ 4\) |
| (A) |
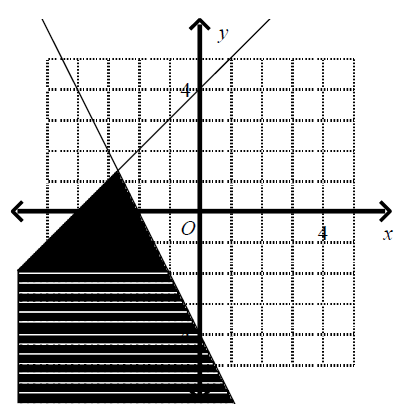 |
| (B) |
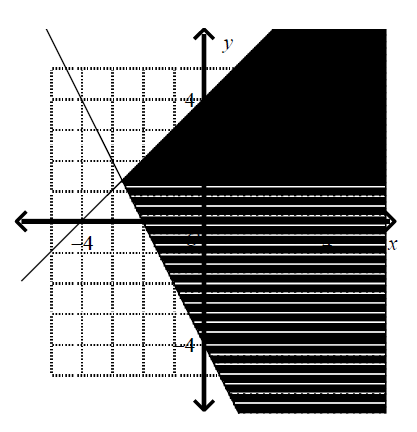 |
| (C) |
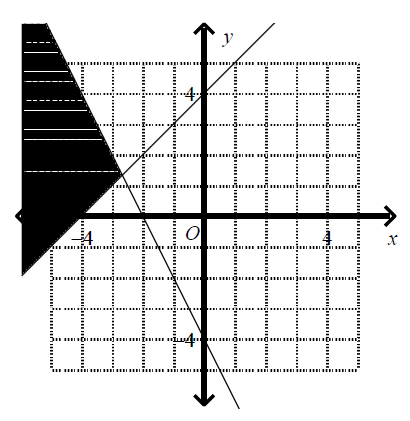 |
| (D) |
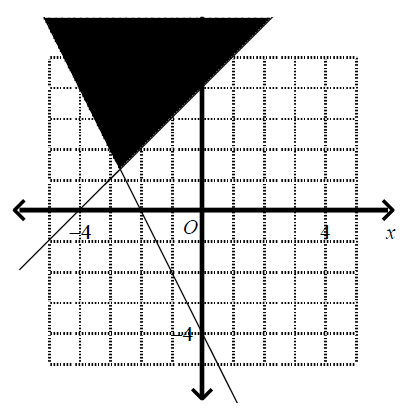 |
| 14- |
A bank is offering \(4.5\%\) simple interest on a savings account. If you deposit \($8,000\), how much interest will you earn in five years? |
| (A) |
\($360\) |
| (B) |
\($720\) |
| (C) |
\($1800\) |
| (D) |
\($3600\) |
| 15- |
A card is drawn at random from a standard \(52–\)card deck, what is the probability that the card is of Hearts? (The deck includes \(13\) of each suit clubs, diamonds, hearts, and spades) |
| (A) |
\(\frac{1}{3}\) |
| (B) |
\(\frac{1}{4}\) |
| (C) |
\(\frac{1}{6}\) |
| (D) |
\(\frac{1}{52}\) |
| 16- |
How long does a \(420–\)miles trip take moving at \(50\) miles per hour (mph)? |
| (A) |
\(4\) hours |
| (B) |
\(6\) hours and \(24\) minutes |
| (C) |
\(8\) hours and \(24\) minutes |
| (D) |
\(8\) hours and \(30\) minutes |
| 17- |
\(11\) yards \(6\) feet and \(4\) inches equals to how many inches? |
| (A) |
\(388\) |
| (B) |
\(468\) |
| (C) |
\(472\) |
| (D) |
\(476\) |
| 18- |
A shirt costing \($200\) is discounted \(15\%\). After a month, the shirt is discounted another \(15\%\). Which of the following expressions can be used to find the selling price of the shirt? |
| (A) |
\((200) \ (0.70)\) |
| (B) |
\((200) \ – \ 200 \ (0.30)\) |
| (C) |
\((200) \ (0.15) \ – \ (200) \ (0.15)\) |
| (D) |
\((200) \ (0.85) \ (0.85)\) |
| 19- |
Which of the following points lies on the line \(2 \ x \ + \ 4 \ y = 10\) |
| (A) |
\((2, \ 1)\) |
| (B) |
\((– \ 1, \ 3)\) |
| (C) |
\((– \ 2, \ 2)\) |
| (D) |
\((2, \ 2)\) |
| 20- |
\(5 \ + \ 8 \ × \ (– \ 2) \ – \ \left[ \ 4 \ + \ 22 \ × \ 5 \ \right] \ ÷ \ 6 =\) ?
Write your answer in the box below. |
| (A) |
-30 |
| (B) |
- 30 |
| (C) |
-30 |
| (D) |
- 30 |
| 21- |
The price of a car was \($20,000\) in \(2014, \ $16,000\) in \(2015\) and \($12,800\) in \(2016\). What is the rate of depreciation of the price of car per year? |
| (A) |
\(15\%\) |
| (B) |
\(20\%\) |
| (C) |
\(25\%\) |
| (D) |
\(30\%\) |
| 22- |
What is the equivalent temperature of \(104^°\)F in Celsius?
C \(= \frac{5}{9}\) (F \(– \ 32\)) |
| (A) |
\(32\) |
| (B) |
\(40\) |
| (C) |
\(48\) |
| (D) |
\(68\) |
| 23- |
The square of a number is \(\frac{25}{64}\). What is the cube of that number?
 |
| (A) |
\(\frac{5}{8}\) |
| (B) |
\(\frac{25}{254}\) |
| (C) |
\(\frac{125}{512}\) |
| (D) |
\(\frac{125}{64}\) |
$16.99 $11.99
29% Off*
The Practice You Need to Ace the STAAR Math Test
|
| 24- |
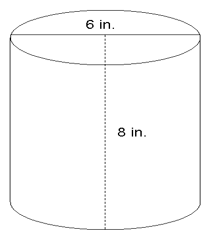
What is the surface area of the cylinder below? |
| (A) |
\(48 \ π\) |
| (B) |
\(57 \ π\) |
| (C) |
\(66 \ π\) |
| (D) |
\(288 \ π\) |
| 25- |
What is the value of \(x\) in the following equation?
\(\frac{2}{3} \ x \ + \ \frac{1}{6}= \frac{1}{3}\) |
| (A) |
\(6\) |
| (B) |
\(\frac{1}{2}\) |
| (C) |
\(\frac{1}{3}\) |
| (D) |
\(\frac{1}{4}\) |
| 26- |
The average of five numbers is \(24\). If a sixth number \(42\) is added, then, what is the new average? |
| (A) |
\(25\) |
| (B) |
\(26\) |
| (C) |
\(27\) |
| (D) |
\(28\) |
| 27- |
Anita’s trick–or–treat bag contains \(12\) pieces of chocolate, \(18\) suckers, \(18\) pieces of gum, \(24\) pieces of licorice. If she randomly pulls a piece of candy from her bag, what is the probability of her pulling out a piece of sucker? |
| (A) |
\(\frac{1}{3}\) |
| (B) |
\(\frac{1}{4}\) |
| (C) |
\(\frac{1}{6}\) |
| (D) |
\(\frac{1}{12}\) |
| 28- |
Which of the following shows the numbers in descending order?
\(\frac{2}{3} , \ 0.68 , \ 67\% , \ \frac{4}{5}\) |
| (A) |
\(67\%, \ 0.68, \frac{2}{3}, \ \frac{4}{5}\) |
| (B) |
\(67\%, \ 0.68, \frac{4}{5}, \ \frac{2}{3}\) |
| (C) |
\(0.68, \ 67\%, \ \frac{2}{3}, \ \frac{4}{5}\) |
| (D) |
\(\frac{2}{3}, \ 67\%, \ 0.68, \ \frac{4}{5}\) |
| 29- |
Mr. Carlos family are choosing a menu for their reception. They have \(3\) choices of appetizers, \(5\) choices of entrees, \(4\) choices of cake. How many different menu combinations are possible for them to choose? |
| (A) |
\(12\) |
| (B) |
\(32\) |
| (C) |
\(60\) |
| (D) |
\(120\) |
| 30- |
Four one – foot rulers can be split among how many users to leave each with \(\frac{1}{6}\) of a ruler? |
| (A) |
\(4\) |
| (B) |
\(6\) |
| (C) |
\(12\) |
| (D) |
\(24\) |
| 31- |
What is the area of a square whose diagonal is \(8\)? |
| (A) |
\(16\) |
| (B) |
\(32\) |
| (C) |
\(36\) |
| (D) |
\(64\) |
| 32- |
The ratio of boys and girls in a class is \(4:7\). If there are \(44\) students in the class, how many more boys should be enrolled to make the ratio \(1:1\)? |
| (A) |
\(8\) |
| (B) |
\(10\) |
| (C) |
\(12\) |
| (D) |
\(14\) |
| 33- |
What is the area of the shaded region?
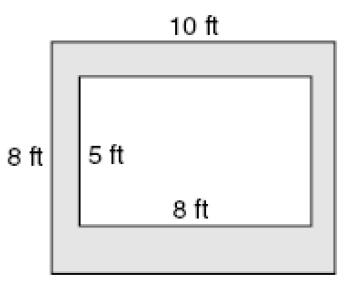 |
| (A) |
\(31\) ft.\(^2\) |
| (B) |
\(40\) ft.\(^2\) |
| (C) |
\(64\) ft.\(^2\) |
| (D) |
\(80\) ft.\(^2\) |
| 34- |
Mr. Jones saves \($2,500\) out of his monthly family income of \($55,000\). What fractional part of his income does he save? |
| (A) |
\(\frac{1}{22}\) |
| (B) |
\(\frac{1}{12}\) |
| (C) |
\(\frac{3}{25}\) |
| (D) |
\(\frac{2}{15}\) |
| 35- |
When a number is subtracted from \(24\) and the difference is divided by that number, the result is \(3\). What is the value of the number? |
| (A) |
\(2\) |
| (B) |
\(4\) |
| (C) |
\(6\) |
| (D) |
\(12\) |
| 36- |
What is the volume of a box with the following dimensions?
Hight \(= 4\) cm Width \(= 5\) cm Length \(= 6\) cm |
| (A) |
\(15\) cm\(^3\) |
| (B) |
\(60\) cm\(^3\) |
| (C) |
\(90\) cm\(^3\) |
| (D) |
\(120\) cm\(^3\) |
| 37- |
In two successive years, the population of a town is increased by \(15\%\) and \(20\%\). What percent of its population is increased after two years? |
| (A) |
\(32\) |
| (B) |
\(35\) |
| (C) |
\(38\) |
| (D) |
\(68\) |
| 38- |
In a school, the ratio of number of boys to girls is \(4:5\). If the number of boys is \(180\), what is the total number of students in the school?
Write your answer in the box below. |
| (A) |
405 |
| (B) |
405 |
| (C) |
405.0 |
| 39- |
How many tiles of \(8\) cm\(^2\) is needed to cover a floor of dimension \(6\) cm by \(24\) cm? |
| (A) |
\(6\) |
| (B) |
\(12\) |
| (C) |
\(18\) |
| (D) |
\(24\) |
| 40- |
The radius of the following cylinder is \(8\) inches and its height is \(12\) inches. What is the surface area of the cylinder?
 |
| (A) |
\(96 \ π\) cm\(^2\) |
| (B) |
\(192 \ π\) cm\(^2\) |
| (C) |
\(320 \ π\) cm\(^2\) |
| (D) |
\(1004.8 \ π\) cm\(^2\) |