What are similar figures
Read,3 minutes
Similar figures are 2 figures with the exact shape. Objects having the exact same size and shape are called congruent objects. For instance, a person’s two hands or the 2 front wheels on a vehicle are a couple of examples of congruent objects. However, objects can be of a similar shape yet have varied sizes. Use the \(∼\) symbol to represent similarity.
Some types of figures or geometrical shapes are similar all the time. Think about circles. Even if the circle’s radius changes all the time, the shape still remains the same. So, you can state that all circles having various radii will be similar to one another. The figure shown below signifies concentric circles whose radii are not the same, however, they are all still similar. Though the circles are shaped the same, the circles’ sizes aren’t the same. So, these circles aren’t congruent.
.png)
Similar Figures Defined
In Mathematics, whenever 2 figures are shaped the same yet have different sizes, they are known as similar figures. For instance, people’s photos having a different size (such as passport, stamp, etc.) are similar objects yet they aren’t congruent. With geometry, 2 similar shapes like similar squares, rectangles, and triangles, are shapes that have dimensions with an equal or a common ratio yet their length or size aren’t the same. A common ratio is known as a scale factor. Additionally, the parallel angles are exactly the same size.
If 2 figures are said to be similar they get signified by using the ‘\(∼\)’ symbol. So, if there are 2 similar triangles, we’ll call them ABC and PQR, then they‘re signified via: \(∆ABC\) \(∼\) \(∆PQR\).
But if 2 triangles are similar to one another, their parallel sides must be in proportion. So,
- \(\frac{AB}{PQ} \ = \ \frac{BC}{QR} \ = \ \frac{AC}{PR}\)
- \(∠A \ = \ ∠P, \ ∠B \ = \ ∠Q, \ ∠C \ = \ ∠R\)
.png)
Area and Volume of Similar Figures
If 2 figures are similar, their parallel sides are proportional. Plus, when the ratio of the triangles’ sides is the same.
So, if you use the ratio of the triangles’ surface areas, this is going to be the same as the square of the ratio of the side. And the ratio of the volume of 2 similar figures is going to be the same as the cube of the ratio of the sides’ length.
Note: It is referring to the ratios, not the figures’ surface area and volume.
So, dependent on the above statements, the scale factors of the area and volumes’ scale factors can be shown like this:
\(SF_{A} \ = \ SF^2\)
\(SF_{V} \ = \ SF^3\)
in which \(SF_{A}\) is the surface area’s scale factor and \(SF_{V}\) is the volume’s scale factor.
Examples of Similar Figures
Look at the below figures. They all are similar to one another, since their shapes are the same, yet they’re not considered to be congruent. You have to remember that when someone says there are similar figures, it is based on shape alone, not counting the sizes of the objects. So, it can be concluded that while all the congruent figures will be similar, all the similar figures aren’t going to be congruent.
.png)
If you take all the similar figures, you are able to state that for any n-sided polygon, its inclination angles of the line segments are the same all the time, no matter what size the figure is. So, for any 2 n-sided polygons with the same number of sides, one can state they’re similar when:
- Corresponding angles of both polygons are equal, as well as
- Corresponding sides of both polygons will be in the exact same ratio.
So, congruence is a distinct example of similarity whenever the ratio of the sides of a figure is \(1\). Which means, whenever 2 similar figures are congruent, the corresponding length of their sides is equal since the ratio of the parallel sides is \(1\).
Free printable Worksheets
Exercises for Similar Figures
1) \(33 : 36 = 11 : x \)
2) \(63 : 84 = 3 : x \)
3) \(69 : 87 = 23 : x \)
4) \(30 : 60 = 1 : x \)
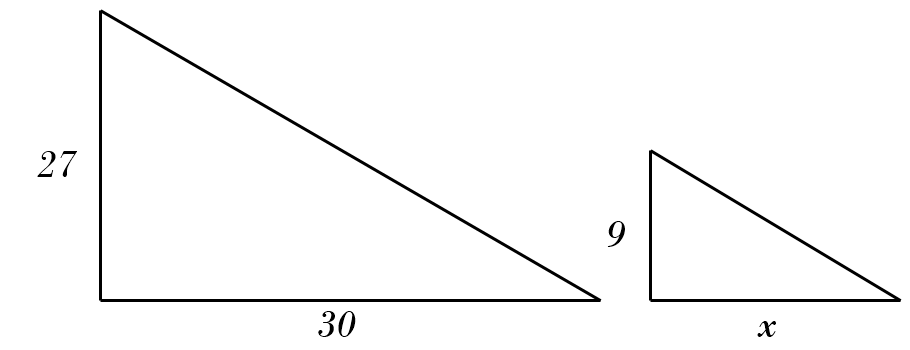
5) \(27 : 30 = 9 : x \)
6) \(98 : 105 = 14 : x \)
7) \(52 : 108 = 13 : x \)
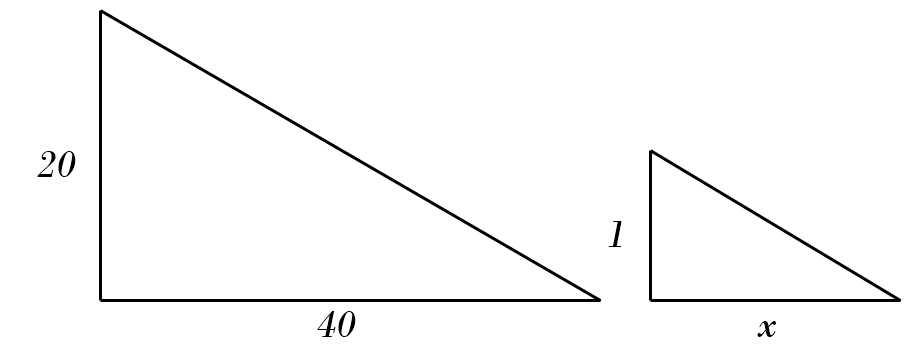
8) \(20 : 40 = 1 : x \)
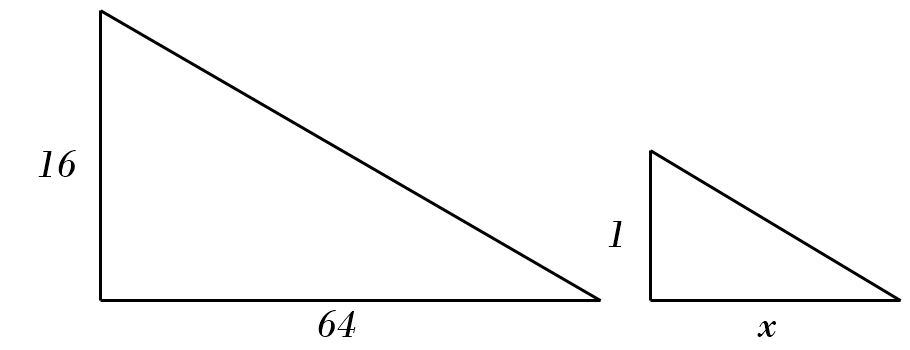
9) \(16 : 64 = 1 : x \)
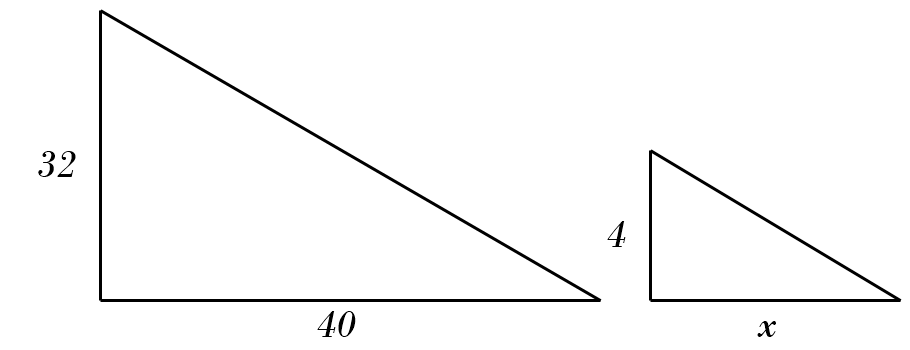
10) \(32 : 40 = 4 : x \)
1) \(33 : 36 = 11 : x \)\( \color{red}{\Rightarrow \ x = \frac{36}{33 \div 11} = 12} \)
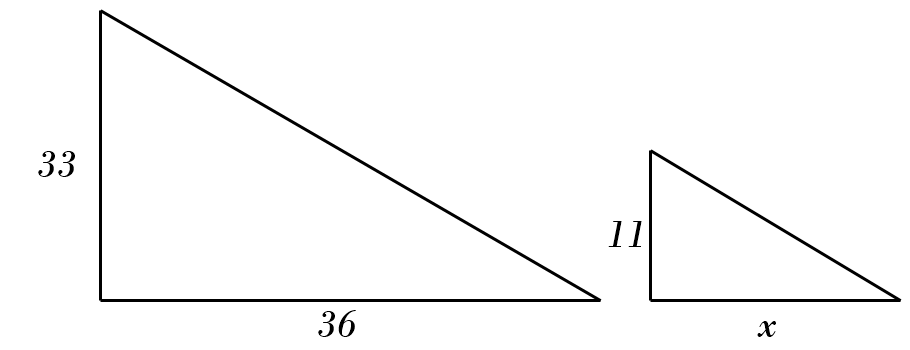
2) \(63 : 84 = 3 : x \)\( \color{red}{\Rightarrow \ x = \frac{84}{63 \div 3} = 4} \)
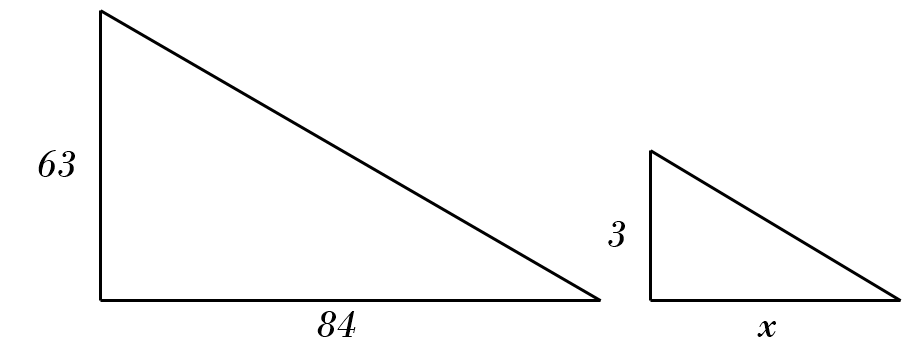
3) \(69 : 87 = 23 : x \)\( \color{red}{\Rightarrow \ x = \frac{87}{69 \div 23} = 29} \)
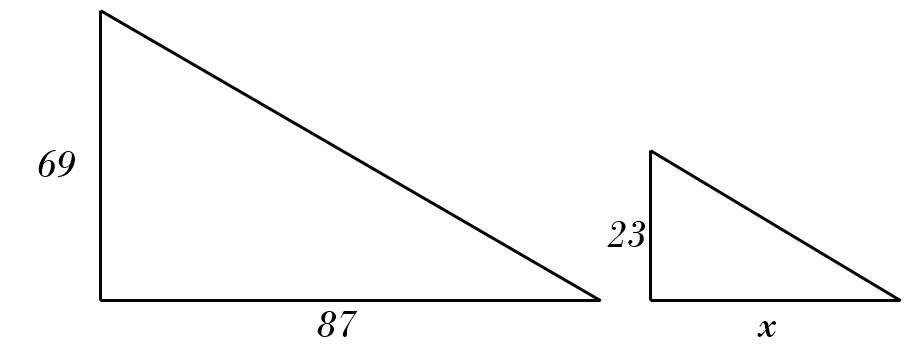
4) \(30 : 60 = 1 : x \)\( \color{red}{\Rightarrow \ x = \frac{60}{30 \div 1} = 2} \)
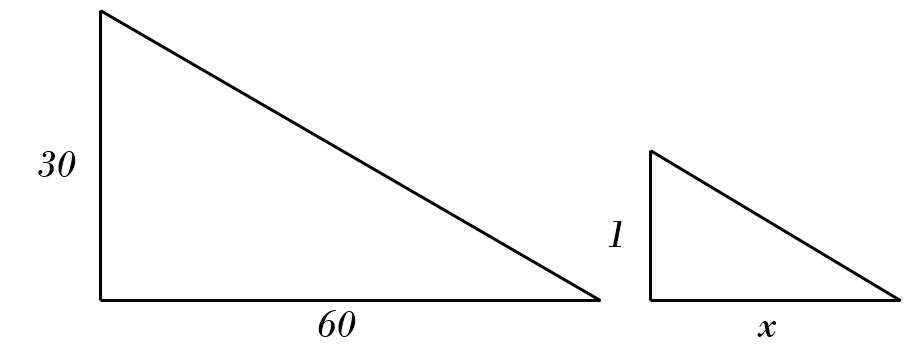
5) \(27 : 30 = 9 : x \)\( \color{red}{\Rightarrow \ x = \frac{30}{27 \div 9} = 10} \)
6) \(98 : 105 = 14 : x \)\( \color{red}{\Rightarrow \ x = \frac{105}{98 \div 14} = 15} \)
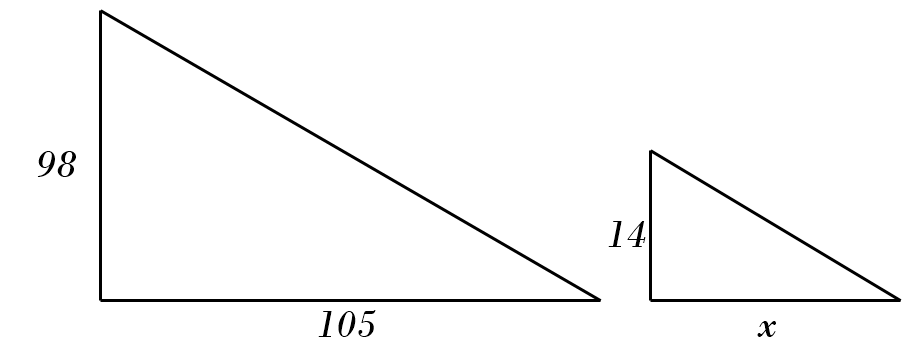
7) \(52 : 108 = 13 : x \)\( \color{red}{\Rightarrow \ x = \frac{108}{52 \div 13} = 27} \)
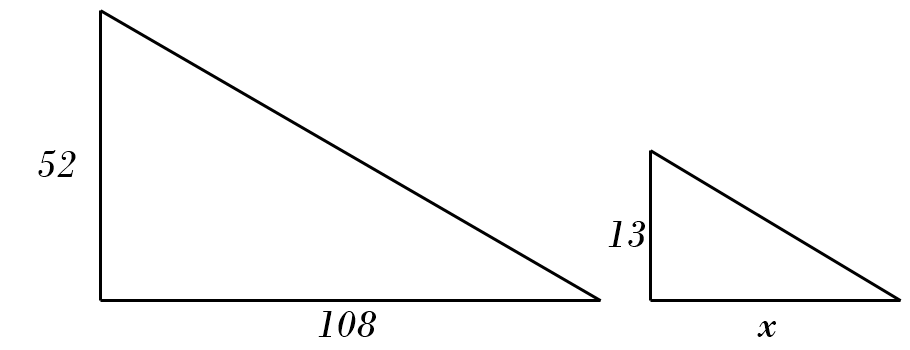
8) \(20 : 40 = 1 : x \)\( \color{red}{\Rightarrow \ x = \frac{40}{20 \div 1} = 2} \)
9) \(16 : 64 = 1 : x \)\( \color{red}{\Rightarrow \ x = \frac{64}{16 \div 1} = 4} \)
10) \(32 : 40 = 4 : x \)\( \color{red}{\Rightarrow \ x = \frac{40}{32 \div 4} = 5} \)
Similar Figures Quiz