|
ACT Mathematics
Practice Test 3 60 questions Total time for this section: 60 Minutes You may use a scientific calculator on this test.
|
| 1- |
What is the median of these numbers? \(3, 10, 13, 8, 15, 19, 5\) |
| (A) |
\(8\) |
| (B) |
\(10\) |
| (C) |
\(5\) |
| (D) |
\(13\) |
| (E) |
\(19\) |
| 2- |
What is the area of a square whose diagonal is \(10\) cm? |
| (A) |
\(25\) cm\(^2\) |
| (B) |
\(30\) cm\(^2\) |
| (C) |
\(125\) cm\(^2\) |
| (D) |
\(100\) cm\(^2\) |
| (E) |
\(50\) cm\(^2\) |
| 3- |
David’s current age is \(42\) years, and Ava’s current age is \(6\) years. In how many years David’s age will be \(4\) times Ava’s age? |
| (A) |
\(4\) |
| (B) |
\(6\) |
| (C) |
\(8\) |
| (D) |
\(10\) |
| (E) |
\(14\) |
| 4- |
How long does a \(360–\)miles trip take moving at \(50\) miles per hour (mph)? |
| (A) |
\(8\) hours and \(10\) minutes |
| (B) |
\(8\) hours |
| (C) |
\(7\) hours and \(24\) minutes |
| (D) |
\(7\) hours and \(12\) minutes |
| (E) |
\(9\) hours and \(12\) minutes |
| 5- |
The marked price of a computer is D dollar. Its price decreased by \(30\%\) in January and later increased by \(10\%\) in February. What is the final price of the computer in D dollar? |
| (A) |
\(0.77\) D |
| (B) |
\(0.80\) D |
| (C) |
\(0.88\) D |
| (D) |
\(0.70\) D |
| (E) |
\(0.90\) D |
| 6- |
Which is the correct statement? |
| (A) |
\(\frac{3}{4} \ > \ 0.8\) |
| (B) |
\(10\% = \frac{2}{5}\) |
| (C) |
\(3 \ < \ \frac{5}{2}\) |
| (D) |
\(\frac{5}{6} \ > \ 0.8\) |
| (E) |
None of them above |
| 7- |
What is the solution of the following inequality?
\(|x \ - \ 12| \ ≤ \ 4\) |
| (A) |
\(7 \ ≤ \ x \ ≤ \ 13\) |
| (B) |
\(10 \ ≤ \ x \ ≤ \ 12\) |
| (C) |
\(8 \ ≤ \ x \ ≤ \ 16\) |
| (D) |
\(8 \ ≤ \ x \) |
| (E) |
\( x \ ≤ \ 16\) |
| 8- |
The number \(42.5\) is \(2,000\) times greater than which of the following numbers? |
| (A) |
\(0.02678\) |
| (B) |
\(0.04498\) |
| (C) |
\(0.02125\) |
| (D) |
\(0.03864\) |
| (E) |
\(0.02018\) |
| 9- |
How many tiles of \(6\) cm\(^2\) is needed to cover a floor of dimension \(9\) cm by \(36\) cm? |
| (A) |
\(58\) |
| (B) |
\(44\) |
| (C) |
\(62\) |
| (D) |
\(54\) |
| (E) |
\(60\) |
| 10- |
Right triangle ABC is shown below. Which of the following is true for all possible values of angle and ?
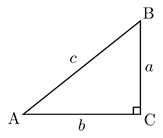 |
| (A) |
cos \(A =\) cos \(B\) |
| (B) |
cos \(A =\) tan \(B\) |
| (C) |
cos \(A =\) sin \(B\) |
| (D) |
tan \(A =1\) |
| (E) |
cot \(A =\) sin \(B\) |
| 11- |
If \(40\%\) of a class are girls, and \(30\%\) of girls play tennis, what percent of the class play tennis? |
| (A) |
\(18\%\) |
| (B) |
\(15\%\) |
| (C) |
\(11\%\) |
| (D) |
\(12\%\) |
| (E) |
\(26\%\) |
| 12- |
\(5^{\frac{7}{3}} \ × \ 5^{\frac{2}{3}} =\) |
| (A) |
\(5^{\frac{5}{2}}\) |
| (B) |
\(5^5\) |
| (C) |
\(5^2\) |
| (D) |
\(5^{\frac{2}{5}}\) |
| (E) |
\(5^{\frac{1}{5}}\) |
| 13- |
A company pays its employer \($6500\) plus \(4\%\) of all sales profit. If \(x\) is the number of all sales profit, which of the following represents the employer’s revenue? |
| (A) |
\(0.04 \ x \ - \ 6500\) |
| (B) |
\(0.96 \ x \ - \ 6500\) |
| (C) |
\(0.96 \ x \ + \ 6500\) |
| (D) |
\(0.04 \ x \) |
| (E) |
\(0.04 \ x \ + \ 6500\) |
| 14- |
\(6\) liters of water are poured into an aquarium that's \(20\) cm long, \(5\) cm wide, and \(90\) cm high. How many cm will the water level in the aquarium rise due to this added water? (\(1\) liter of water \(= 1000\) cm\(^3\)) |
| (A) |
\(120\) cm |
| (B) |
\(90\) cm |
| (C) |
\(80\) cm |
| (D) |
\(60\) cm |
| (E) |
\(30\) cm |
| 15- |
Five years ago, Amy was four times as old as Mike was. If Mike is \(12\) years old now, how old is Amy? |
| (A) |
\(33\) |
| (B) |
\(25\) |
| (C) |
\(22\) |
| (D) |
\(38\) |
| (E) |
\(41\) |
| 16- |
What is the value of \(x\) in the following figure?
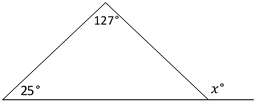 |
| (A) |
\(145^\circ\) |
| (B) |
\(152^\circ\) |
| (C) |
\(122^\circ\) |
| (D) |
\(136^\circ\) |
| (E) |
\(158^\circ\) |
|
| 17- |
If \(|a| \ < \ 1\), then which of the following is true? \((b \ > \ 0)\)?
I. \(– \ b \ < \ b \ a \ < \ b\)
II. \(- \ a \ < \ a^2 \ < \ a\) if \(a \ < \ 0\)
III. \(- \ 5 \ <2 \ a \ - \ 3 \ < \ - \ 1\) |
| (A) |
I only |
| (B) |
II only |
| (C) |
I and III only |
| (D) |
III only |
| (E) |
I, II and III |
| 18- |
If \(x\) is a real number, and if \(x^3 \ + \ 18=130\), then \(x\) lies between which two consecutive integers? |
| (A) |
\(1\) and \(2\) |
| (B) |
\(2\) and \(3\) |
| (C) |
\(3\) and \(4\) |
| (D) |
\(4\) and \(5\) |
| (E) |
\(5\) and \(6\) |
| 19- |
From the figure, which of the following must be true? (figure not drawn to scale)
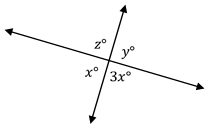 |
| (A) |
\(y \ + \ 2 \ x=𝑧\) |
| (B) |
\(y \ + \ 4 \ x=𝑧\) |
| (C) |
\(y=𝑧\) |
| (D) |
\(x=𝑧\) |
| (E) |
\(2 \ x=𝑧\) |
| 20- |
What is the value of \(y\) in the following system of equation?
\(2 \ x \ - \ y= \ - \ 48\)
\(- \ x \ + \ 2 \ y= 12\) |
| (A) |
\(- \ 5\) |
| (B) |
\(- \ 10\) |
| (C) |
\(- \ 8\) |
| (D) |
\(5\) |
| (E) |
\(8\) |
| 21- |
When \(30\%\) of \(60\) is added to \(15\%\) of \(420,\) the resulting number is: |
| (A) |
\(92\) |
| (B) |
\(81\) |
| (C) |
\(120\) |
| (D) |
\(143\) |
| (E) |
\(75\) |
| 22- |
If a box contains red and blue balls in ratio of \(5 : 3\), how many red balls are there if \(90 \) blue balls are in the box? |
| (A) |
\(150\) |
| (B) |
\(120\) |
| (C) |
\(100\) |
| (D) |
\(80\) |
| (E) |
\(200\) |
| 23- |
Simplify \((– \ 4 \ + \ 5 \ i) \ (2 \ + \ 7\ i)\) |
| (A) |
\(- \ 49 \ - \ 18 \ i\) |
| (B) |
\(39 \ - \ 18 \ i\) |
| (C) |
\(40 \ + \ 22\ i\) |
| (D) |
\(25 \ i\) |
| (E) |
\(25 \ i \ + \ 49\) |
| 24- |
Which of the following has the same period and two times the amplitude of graph?
\(y =\) cos \(x\)? |
| (A) |
\(y=\) cos \((x \ + 2)\) |
| (B) |
\(y=4\ + \) cos \( x\) |
| (C) |
\(y=\) cos \(2 \ x\) |
| (D) |
\(y=4\) cos \(2 \ x\) |
| (E) |
\(y=2 \ + 2\) cos \( x\) |
| 25- |
A ladder leans against a wall forming a \(60^ᵒ\) angle between the ground and the ladder. If the bottom of the ladder is \(30\) feet away from the wall, how long is the ladder? |
| (A) |
\(50\) feet |
| (B) |
\(25\) feet |
| (C) |
\(40\) feet |
| (D) |
\(100\) feet |
| (E) |
\(125\) feet |
| 26- |
What is the surface area of the cylinder below?
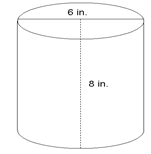 |
| (A) |
\(44 \ π\) in\(^2\) |
| (B) |
\(55 \ π\) in\(^2\) |
| (C) |
\(66 \ π\) in\(^2\) |
| (D) |
\(77\ π\) in\(^2\) |
| (E) |
\(88 \ π\) in\(^2\) |
| 27- |
Simplify:
\(5 \ x^2 \ + \ 2 \ y^5 \ - \ x^2 \ - \ 6 \ z^3 \ + \ 3 \ y^2 \ + \ 4 \ x^3 \ - \ 7 \ y^5 \ + \ 8 \ z^3\) |
| (A) |
\(2 \ x^2 \ + \ 4 \ x^3 \ + \ 4 \ y^2 \ - \ 8 \ y^5 \ + \ 2 \ z^3\) |
| (B) |
\(6 \ x^2 \ + \ 3 \ x^3 \ + \ 4 \ y^2 \ - \ 8 \ y^5 \) |
| (C) |
\(4 \ x^2 \ + \ 4 \ x^3 \ + \ 3 \ y^2 \ - \ 5 \ y^5 \ + \ 2 \ z^3\) |
| (D) |
\( x^3 \ + \ 3 \ y^2 \ - \ 8 \ y^5 \ + \ 3 \ z^3\) |
| (E) |
\(4 \ x^2 \ + \ 5 \ y^5 \ + \ 2 \ z^3\) |
| 28- |
A bag contains \(18\) balls: two green, five black, eight blue, a brown, a red and one white. If \(17\) balls are removed from the bag at random, what is the probability that a brown ball has been removed? |
| (A) |
\(\frac{17}{18}\) |
| (B) |
\(\frac{1}{18}\) |
| (C) |
\(\frac{1}{17}\) |
| (D) |
\(\frac{18}{17}\) |
| (E) |
\(17\) |
| 29- |
Which of the following shows the numbers in increasing order? |
| (A) |
\(\frac{3}{4}, \frac{5}{7}, \frac{8}{13}, \frac{2}{5}\) |
| (B) |
\(\frac{3}{4}, \frac{8}{13}, \frac{5}{7}, \frac{2}{5}\) |
| (C) |
\(\frac{8}{13}, \frac{3}{4}, \frac{5}{7}, \frac{2}{5}\) |
| (D) |
\(\frac{2}{5}, \frac{5}{7}, \frac{8}{13}, \frac{3}{4}\) |
| (E) |
\(\frac{5}{7}, \frac{8}{13}, \frac{2}{5}, \frac{3}{4}\) |
| 30- |
If a tree casts a \(24–\)foot shadow at the same time that a \(6\) feet yardstick casts a \(3–\)foot shadow, what is the height of the tree?
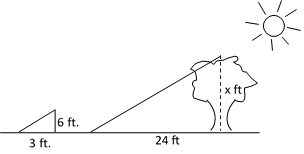 |
| (A) |
\(36\) ft. |
| (B) |
\(52\) ft. |
| (C) |
\(24\) ft. |
| (D) |
\(48\) ft. |
| (E) |
\(38\) ft. |
|
| 31- |
From last year, the price of gasoline has increased from \($1.20\) per gallon to \($1.80\) per gallon. The new price is what percent of the original price? |
| (A) |
\(180\%\) |
| (B) |
\(200\%\) |
| (C) |
\(150\%\) |
| (D) |
\(120\%\) |
| (E) |
\(100\%\) |
| 32- |
If \((x \ - \ 25)^3=125\) which of the following could be the value of \((x \ - \ 21) \ (x \ - \ 10)\)? |
| (A) |
\(180\) |
| (B) |
\(112\) |
| (C) |
\(320\) |
| (D) |
\(220\) |
| (E) |
\(150\) |
| 33- |
What are the values of mode and median in the following set of numbers?
\(1,2,2,5,4,4,3,3,3,1,1\) |
| (A) |
\(1, \ 3\) Median: \(3\) |
| (B) |
\(1, \ 2\) Median: \(2\) |
| (C) |
\(2, \ 3\) Median: \(2\) |
| (D) |
\(1, \ 3\) Median: \(2.5\) |
| (E) |
\( 3\) Median: \(3\) |
| 34- |
If \( x \ \begin{bmatrix}2 & 0 \\0 & 3 \end{bmatrix} = \begin{bmatrix}x \ + \ 2 \ y \ - \ 4 & 0 \\0 & 2 \ y \ + \ 12 \end{bmatrix}\), what is the product of \(x\) and \(y\)? |
| (A) |
\(24\) |
| (B) |
\(36\) |
| (C) |
\(48\) |
| (D) |
\(52\) |
| (E) |
\(61\) |
| 35- |
Removing which of the following numbers will change the average of the numbers to \(6\)?
\(2, 4, 6, 8, 10, 12\) |
| (A) |
\(2\) |
| (B) |
\(4\) |
| (C) |
\(6\) |
| (D) |
\(10\) |
| (E) |
\(12\) |
| 36- |
If \(f(x) = 4 \ + \ x\) and \(g(x) = \ – \ x^2 \ + \ 3 \ – \ 2 \ x\), then find \((g \ – \ f)(x)\)? |
| (A) |
\(– \ x^2 \ + \ 2 \ x \ – \ 1\) |
| (B) |
\(– \ x^2 \ - \ 3 \ x\) |
| (C) |
\( x^2 \ + \ 3 \ x \ – \ 2\) |
| (D) |
\( 2 \ x^2 \ + \ 4 \ x \ – \ 2\) |
| (E) |
\(– \ x^2 \ – \ 3 \ x \ – \ 1\) |
| 37- |
If \(50\%\) of \(x\) equal to \(40\%\) of \(20\), then what is the value of \((x \ + \ 1)^2\)? |
| (A) |
\(169\) |
| (B) |
\(225\) |
| (C) |
\(25\) |
| (D) |
\(289\) |
| (E) |
\(324\) |
| 38- |
If \(\frac{2 \ x}{18}=\frac{x \ - \ 2}{6}, x=\) |
| (A) |
\(4\) |
| (B) |
\(6\) |
| (C) |
\(8\) |
| (D) |
\(\frac{1}{6}\) |
| (E) |
\(\frac{1}{4}\) |
| 39- |
In \(1999\), the average worker's income increased \($2,500\) per year starting from \($25,000\) annual salary. Which equation represents income greater than average? (\(I =\) income, \(x =\) number of years after \(1999\)) |
| (A) |
\(I \ > \ 2500 \ x \ + \ 50000\) |
| (B) |
\(I \ < \ 5000 \ x \ + \ 50000\) |
| (C) |
\(I \ > \ 2500 \ x \ - \ 25000\) |
| (D) |
\(I \ < \ 2500 \ x \ + \ 25000\) |
| (E) |
\(I \ > \ 2500 \ x \ + \ 25000\) |
| 40- |
In five successive hours, a car travels \(32\) km, \(40\) km, \(51\) km, \(39\) km and \(53\) km. In the next five hours, it travels with an average speed of \(50\) km per hour. Find the total distance the car traveled in \(10\) hours. |
| (A) |
\(425\) km |
| (B) |
\(386\) km |
| (C) |
\(412\) km |
| (D) |
\(465\) km |
| (E) |
\(491\) km |
| 41- |
A chemical solution contains \(3\%\) alcohol. If there is \(24\) ml of alcohol, what is the volume of the solution? |
| (A) |
\(600\) ml |
| (B) |
\(500\) ml |
| (C) |
\(200\) ml |
| (D) |
\(250\) ml |
| (E) |
\(800\) ml |
| 42- |
If cot \(\theta = \frac{12}{5}\) and sin \(\theta \ > \ 0\), then cos \(\theta =\)? |
| (A) |
\(- \ \frac{12}{13}\) |
| (B) |
\(- \ \frac{13}{12}\) |
| (C) |
\(- \ \frac{5}{12}\) |
| (D) |
\( \frac{12}{13}\) |
| (E) |
\( \frac{13}{12}\) |
| 43- |
In the \(x \ y-\)plane, the point \((5, 2)\) and \((6, 4)\) are on line A. Which of the following equations of lines is parallel to line A? |
| (A) |
\(y= x\) |
| (B) |
\(y= 2\) |
| (C) |
\(y=2 \ x\) |
| (D) |
\(y=- \ 2 \ x\) |
| (E) |
\(y=\frac{1}{2} \ x\) |
| 44- |
If \(f(x)=3^x\) and \(g(x)=\log_{3}{x}\), which of the following expressions is equal to \(f(3g(p))\)? |
| (A) |
\(P^9\) |
| (B) |
\(P^6\) |
| (C) |
\(3 \ P^2\) |
| (D) |
\(\frac{P}{3}\) |
| (E) |
\(P^3\) |
| 45- |
The result of a research shows the number of men and women in four cities of a country.
What's the maximum ratio of the number of women to number of men in each city?
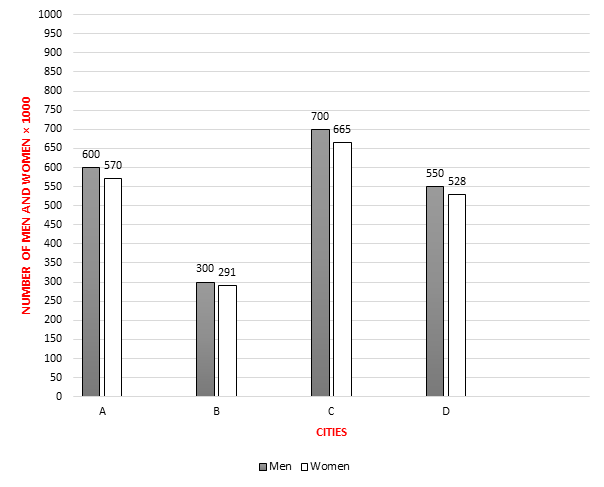 |
| (A) |
\(0.98\) |
| (B) |
\(0.97\) |
| (C) |
\(0.96\) |
| (D) |
\(0.95\) |
| (E) |
\(0.94\) |
| 46- |
The result of a research shows the number of men and women in four cities of a country.
What's the ratio of the percentage of men in city A to percentage of women in city C?
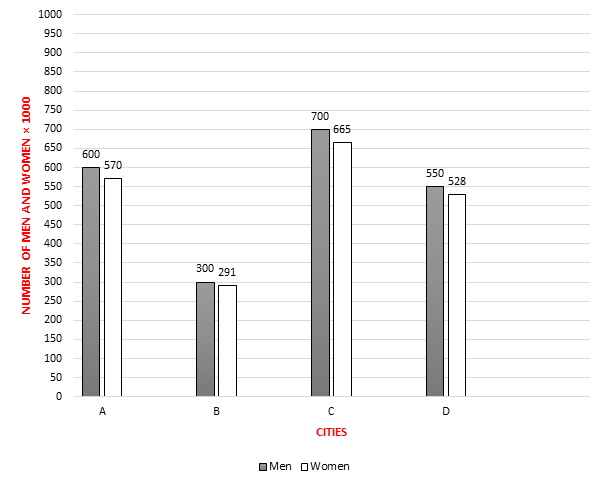 |
| (A) |
\(\frac{19}{20}\) |
| (B) |
\(\frac{19}{2}\) |
| (C) |
\(1\) |
| (D) |
\(\frac{20}{19}\) |
| (E) |
\(\frac{2}{19}\) |
| (F) |
\(\frac{2}{19}\) |
| 47- |
The result of a research shows the number of men and women in four cities of a country.
How many women should be added to city D to change the ratio of women to men to \(1.2\)?
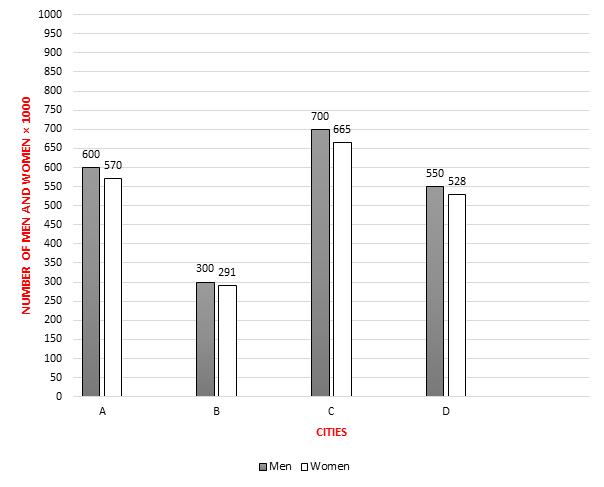 |
| (A) |
\(135\) |
| (B) |
\(134\) |
| (C) |
\(133\) |
| (D) |
\(132\) |
| (E) |
\(131\) |
| 48- |
\(120\) is equal to: |
| (A) |
\(20 \ − \ (4 \ × \ 10) \ + \ (6 \ × \ 30)\) |
| (B) |
\((\frac{11}{8} \ × \ 72) \ + \ (\frac{125}{5})\) |
| (C) |
\(((\frac{30}{4} \ + \ \frac{13}{2}) \ × \ 7) \ − \ \frac{11}{2} \ + \ \frac{110}{4}\) |
| (D) |
\((2 \ × \ 10) \ + \ (50 \ × \ 1.5) \ + \ 15\) |
| (E) |
\(\frac{481}{6} \ + \ \frac{121}{3}\) |
| 49- |
Which of the following points lies on the line \(2 \ x \ + \ 4 \ y = 12\)? |
| (A) |
\((2, 2)\) |
| (B) |
\((– \ 1, 3)\) |
| (C) |
\((– \ 2, 2)\) |
| (D) |
\((2, 3)\) |
| (E) |
\((2, 8)\) |
| 50- |
In the following equation when \(z\) is divided by \(2\), what is the effect on \(x\)?
\(x=\frac{5 \ y \ + \ \frac{r}{r \ + \ 2}}{\frac{4}{z}}\) |
| (A) |
\(x\) is divided by \(3\) |
| (B) |
\(x\) is multiplied by \(3\) |
| (C) |
\(x\) is multiplied by \(2\) |
| (D) |
\(x\) is divided by \(2\) |
| (E) |
\(x\) does not change |
| 51- |
If \(y = 3 \ a \ b \ + \ 4 \ b^3\), what is \(y\) when \(a = 3\) and \(b = 3\)? |
| (A) |
\(102\) |
| (B) |
\(78\) |
| (C) |
\(108\) |
| (D) |
\(24\) |
| (E) |
\(36\) |
| 52- |
If tangent of an angel \(β\) is \(2\), then the cotangent of angle \(β\) is: |
| (A) |
\(1\) |
| (B) |
\(\frac{1}{2}\) |
| (C) |
\(2\) |
| (D) |
\(0\) |
| (E) |
\(\frac{1}{4}\) |
| 53- |
When point A \((5, 3)\) is reflected over the \(y-\)axis to get the point B, what are the coordinates of point B? |
| (A) |
\((- \ 5, 3)\) |
| (B) |
\((- \ 5, - \ 3)\) |
| (C) |
\((5, - \ 3)\) |
| (D) |
\((5, 3)\) |
| (E) |
\((0, 3)\) |
| 54- |
If \(f(x)=2 \ x^3 \ - \ 3 \ x^2 \ + \ 4 \ x\) and \(g(x)= \ - \ 2\), what is the value of \(f(g(x))\)? |
| (A) |
\(- \ 36\) |
| (B) |
\(- \ 22\) |
| (C) |
\(0\) |
| (D) |
\(32\) |
| (E) |
\(18\) |
| 55- |
A boat sails \(40\) miles south and then \(30\) miles east. How far is the boat from its start point? |
| (A) |
\(50\) miles |
| (B) |
\(80\) miles |
| (C) |
\(40\) miles |
| (D) |
\(70\) miles |
| (E) |
\(60\) miles |
| 56- |
If the area of trapezoid is \(100\), what is the perimeter of the trapezoid?
 |
| (A) |
\(24\) |
| (B) |
\(32\) |
| (C) |
\(18\) |
| (D) |
\(29\) |
| (E) |
\(36\) |
| 57- |
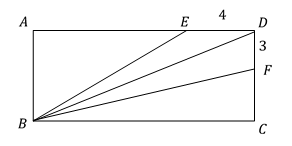
In the following figure, ABCD is a rectangle, and E and F are points on AD and DC, respectively. The area of \(\triangle\)BED is \(18\), and the area of \(\triangle\)BDF is \(24\). What is the perimeter of the rectangle?
 |
| (A) |
\(70\) |
| (B) |
\(45\) |
| (C) |
\(50\) |
| (D) |
\(63\) |
| (E) |
\(54\) |
| 58- |
A rope weighs \(500\) grams per meter of length. What is the weight in kilograms of \(13.2\) meters of this rope? (\(1\) kilograms \(= 1000\) grams) |
| (A) |
\(5.4\) kg |
| (B) |
\(6.6\) kg |
| (C) |
\(7.2\) kg |
| (D) |
\(4.9\) kg |
| (E) |
\(6.1\) kg |
| 59- |
\(z\) is \(x\%\) of what number? |
| (A) |
\(\frac{100 \ z}{x} \) |
| (B) |
\(\frac{1 \ z}{100 \ x} \) |
| (C) |
\(\frac{z}{\frac{1}{100} \ x} \) |
| (D) |
\(\frac{100 \ x}{z} \) |
| (E) |
\(\frac{x \ z}{100} \) |
| 60- |
A number is chosen at random from \(1\) to \(25\). Find the probability of not selecting a composite number. |
| (A) |
\(1\) |
| (B) |
\(0\) |
| (C) |
\(\frac{1}{5}\) |
| (D) |
\(\frac{5}{2}\) |
| (E) |
\(\frac{2}{5}\) |