|
ACT Mathematics
Practice Test 4
60 questions
Total time for this section: 60 Minutes
You can use a scientific calculator on this test.
|
| 1- |
If the interior angles of a quadrilateral are in the ratio \(1:2:3:4\), what is the measure of the smallest angle? |
| (A) |
\(36^\circ\) |
| (B) |
\(72^\circ\) |
| (C) |
\(108^\circ\) |
| (D) |
\(144^\circ\) |
| (E) |
\(168^\circ\) |
| 2- |
What is the value of x in the following system of equations?
\(2 \ x \ + \ 3 \ y=12\)
\(4 \ x \ - \ 4 \ y= \ - \ 16\) |
| (A) |
\(0 \) |
| (B) |
\(1 \) |
| (C) |
\(2\) |
| (D) |
\(- \ 2\) |
| (E) |
\(- \ 1\) |
| 3- |
If sin A \(= \frac{1}{5}\) in a right triangle and the angle A is an acute angle, then what is cos A? |
| (A) |
\(\frac{\sqrt{6}}{5}\) |
| (B) |
\(\frac{\sqrt{6}}{10}\) |
| (C) |
\(\frac{2 \ \sqrt{6}}{5}\) |
| (D) |
\(\frac{5 }{\sqrt{6}}\) |
| (E) |
\(\frac{5 }{2 \ \sqrt{6}}\) |
| 4- |
The ratio of boys to girls in a school is \(3:4\). If there are \(560\) students in a school, how many boys are in the school. |
| (A) |
\(350\) |
| (B) |
\(410\) |
| (C) |
\(120\) |
| (D) |
\(420\) |
| (E) |
\(510\) |
| 5- |
If \(f(x) = 2 \ x \ – \ 1\) and \(g(x) = x^2 \ + \ 2 \ x\), then find \((\frac{f}{g})(x)\). |
| (A) |
\(\frac{2 \ x \ − \ 1}{x^2 \ + \ 2 \ x}\) |
| (B) |
\(\frac{2 \ x \ + \ 1}{x^2 \ - \ 2 \ x}\) |
| (C) |
\(\frac{x^2 \ - \ 2 \ x}{2 \ x \ + \ 1}\) |
| (D) |
\(\frac{x^2 \ + \ 2 \ x}{2 \ x \ - \ 1}\) |
| (E) |
\(\frac{1}{2 \ x \ - \ 1}\) |
| 6- |
If \((x \ - \ 2)^2 \ + \ 1 \ > \ 3 \ x \ - \ 1\), then \(x\) can equal which of the following? |
| (A) |
\(1\) |
| (B) |
\(6\) |
| (C) |
\(8\) |
| (D) |
\(3\) |
| (E) |
\(4\) |
| 7- |
In the standard \((x, y)\) coordinate system plane, what is the area of the circle with the following equation?
\((x \ + \ 2)^2 \ + \ (y \ - \ 4)^2=25\) |
| (A) |
\(31\ π\) |
| (B) |
\(36\ π\) |
| (C) |
\(5\ π\) |
| (D) |
\(25\ π\) |
| (E) |
\(16 \ π\) |
| 8- |
In the standard \((x, y)\) coordinate plane, which of the following lines contains the points
\((3, - \ 5)\) and \((8, 15)\)? |
| (A) |
\(y=\frac{1}{4} \ x \ + \ 13\) |
| (B) |
\(y= \ - \ \frac{1}{4} \ x \ + \ 17\) |
| (C) |
\(y= \ - \ 4 \ x \ + \ 7\) |
| (D) |
\(y=4 \ x \ − \ 17\) |
| (E) |
\(y= 2 \ x \ - \ 11\) |
| 9- |
If the area of a circle is \(49\) square meters, what is its diameter? |
| (A) |
\(\frac{8 \sqrt{π}}{π}\) |
| (B) |
\(\frac{\pi}{8 \sqrt{π}}\) |
| (C) |
\(\frac{\pi}{7 \sqrt{π}}\) |
| (D) |
\(\frac{7\sqrt{π}}{π}\) |
| (E) |
\(\frac{1}{7\sqrt{π}}\) |
| 10- |
A bank is offering \(2.5\%\) simple interest on a savings account. If you deposit \($15,000\), how much interest will you earn in two years? |
| (A) |
\($800\) |
| (B) |
\($700\) |
| (C) |
\($750\) |
| (D) |
\($850\) |
| (E) |
\($900\) |
| 11- |
What is the solution of the following inequality?
\(|x \ - \ 5| \ ≥ \ 4\) |
| (A) |
\(x\ ≥9\) |
| (B) |
\(x≤ 1\) |
| (C) |
\(x\ ≥9 \ ∪ \ x≤ 1\) |
| (D) |
\(x\ ≥9 \ ∪ \ x≤- \ 1\) |
| (E) |
\(x\ ≥ \ - \ 9 \ ∪ \ x≤- \ 1\) |
| 12- |
The length of a rectangle is \(\frac{3}{5}\) times its width. If the width is \(15\), what is the perimeter of this rectangle? |
| (A) |
\(42\) |
| (B) |
\(45\) |
| (C) |
\(48\) |
| (D) |
\(53\) |
| (E) |
\(64\) |
| 13- |
If \(120\%\) of a number is \(90\), then what is \(80\%\) of that number? |
| (A) |
\(70\) |
| (B) |
\(60\) |
| (C) |
\(80\) |
| (D) |
\(65\) |
| (E) |
\(75\) |
| 14- |
In two successive years, the population of a town is increased by \(12\%\) and \(25\%\). What percent of the population is increased after two years? |
| (A) |
\(40\%\) |
| (B) |
\(30\%\) |
| (C) |
\(50\%\) |
| (D) |
\(60\%\) |
| (E) |
\(20\%\) |
| 15- |
If the ratio of home fans to visiting fans in a crowd is \(3:2\) and all \(25,000\) seats in a stadium are filled, how many visiting fans are in attendance? |
| 16- |
A card is drawn at random from a standard \(57–\)card deck, what is the probability that the card is of Hearts? (The deck includes \(12\) of each suit clubs, diamonds, hearts, and spades) |
| (A) |
\(\frac{1}{19}\) |
| (B) |
\(\frac{19}{4}\) |
| (C) |
\(\frac{1}{4}\) |
| (D) |
\(\frac{1}{9}\) |
| (E) |
\(\frac{4}{19}\) |
| 17- |
Simplify:
\(4 \ x^2 \ y^3 \ + \ 5 \ x^3 \ y^5 \ – \ (9 \ x^2 \ y^3 \ – \ 4 \ x^3 \ y^5)\) |
| (A) |
\(7\ x^3\ y^5\ + \ 5 \ x^2\ y^3\) |
| (B) |
\(9\ x^3\ y^5\ -\ 5 \ x^2\ y^3\) |
| (C) |
\(- \ 9\ x^3\ y^5\ + \ 7 \ x^2\ y^3\) |
| (D) |
\(- \ 5\ x^3\ y^5\) |
| (E) |
\(9\ x^3\ y^5\ +\ 9 \ x^2\ y^3\) |
| 18- |
In the figure below, line A is parallel to line B. What is the value of angle \(x\)?
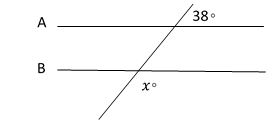 |
| (A) |
\(112\) degree |
| (B) |
\(180\) degree |
| (C) |
\(142\) degree |
| (D) |
\(153\) degree |
| (E) |
\(124\) degree |
| 19- |
If tan\(x=\frac{6}{8}\), then sin \(x=\) |
| (A) |
\(\frac{3}{10}\) |
| (B) |
\(\frac{3}{5}\) |
| (C) |
\(\frac{6}{5}\) |
| (D) |
\(\frac{1}{5}\) |
| (E) |
It cannot be determined from the information given. |
| 20- |
An angle is equal to one fourth of its supplement. What is the measure of that angle? |
| (A) |
\(30\) |
| (B) |
\(42\) |
| (C) |
\(49\) |
| (D) |
\(21\) |
| (E) |
\(36\) |
| 21- |
If \(x \ + \) sin\(^2 \ a \ +\) cos\(^2 \ a=5\), then \(x =\)? |
| (A) |
\(1\) |
| (B) |
\(2\) |
| (C) |
\(3\) |
| (D) |
\(4\) |
| (E) |
\(5\) |
| 22- |
Sophia purchased a sofa for \($474.24\). The sofa is regularly priced at \($624\). What was the percent discount Sophia received on the sofa? |
| (A) |
\(18\%\) |
| (B) |
\(12\%\) |
| (C) |
\(24\%\) |
| (D) |
\(31\%\) |
| (E) |
\(36\%\) |
| 23- |
Which of the following expressions is equal to \(\sqrt{\frac{x^2}{3} \ + \ \frac{x^2}{12}} \)? |
| (A) |
\(\frac{\sqrt{3} }{2 \ \sqrt{5}} \ x\) |
| (B) |
\(\frac{\sqrt{5} }{2 \ \sqrt{3}} \ x\) |
| (C) |
\(\frac{\sqrt{5} }{2 } \ x\) |
| (D) |
\(\frac{\sqrt{5} }{ \sqrt{3}} \ x\) |
| (E) |
\(\frac{2 \ \sqrt{5} }{ \sqrt{3}} \ x\) |
| 24- |
Last week \(18,000\) fans attended a football match. This week three times as many bought tickets, but one sixth of them cancelled their tickets. How many are attending this week? |
| (A) |
\( 54,000\) |
| (B) |
\(35,000\) |
| (C) |
\( 45,000\) |
| (D) |
\(81,000\) |
| (E) |
\(9,000\) |
| 25- |
The average of six consecutive numbers is \(30\). What is the smallest number? |
| (A) |
\(22\) |
| (B) |
\(21.5\) |
| (C) |
\(24\) |
| (D) |
\(25.5\) |
| (E) |
\(27.5\) |
| 26- |
What is the slope of a line that is perpendicular to the line?
\(4 \ x \ - \ 2 \ y=16\)? |
| (A) |
\( \frac{1}{2}\) |
| (B) |
\(2\) |
| (C) |
\(- \ 2\) |
| (D) |
\(− \ \frac{1}{2}\) |
| (E) |
\(1\) |
| 27- |
What is the value of the expression \(5 \ (x \ - \ 2 \ y) \ + \ (2 \ - \ x)^2\) when \(x=2\) and \(y= \ - \ 2\)? |
| (A) |
\(25\) |
| (B) |
\(20\) |
| (C) |
\(35\) |
| (D) |
\(15\) |
| (E) |
\(30\) |
| 28- |
Convert \(320,000\) to scientific notation. |
| (A) |
\(32\ ×\ 10^5\) |
| (B) |
\(32\ ×\ 10^6\) |
| (C) |
\(3.2\ ×\ 10^6\) |
| (D) |
\(3.2\ ×\ 10^4\) |
| (E) |
\(3.2\ ×\ 10^5\) |
| 29- |
If \(\sqrt{8 \ x}=\sqrt{y}\), then \(x=\) |
| (A) |
\(\frac{y}{9}\) |
| (B) |
\(\frac{9}{y}\) |
| (C) |
\(\frac{y}{8}\) |
| (D) |
\(\frac{8}{y}\) |
| (E) |
\(\frac{1}{y}\) |
| 30- |
In following rectangle which statement is true?
 |
| (A) |
Length of AD equal to length BC |
| (B) |
Length of AB equal to length BC |
| (C) |
Length of AB equal to length AD |
| (D) |
The measure of all the angles equals \(180^°\). |
| (E) |
The answer cannot be found from the information given. |
| 31- |
The surface area of a cylinder is \(48 \ π\) cm\(^2\). If its height is \(10\) cm, what is the radius of the cylinder? |
| (A) |
\(2\) cm |
| (B) |
\(4\) cm |
| (C) |
\(5\) cm |
| (D) |
\(7\) cm |
| (E) |
\(1\) cm |
| 32- |
Let \(r\) and \(p\) be constants. If \(x^2 \ + \ 6 \ x \ + \ r\) factors into \((x \ + \ 2) \ (x \ + \ p)\), the values of \(r\) and \(p\) respectively are? |
| (A) |
\(4, 6\) |
| (B) |
\(6, 3\) |
| (C) |
\(4, 8\) |
| (D) |
\(8, 4\) |
| (E) |
The answer cannot be found from the information given. |
| 33- |
In a coordinate plane, triangle ABC has coordinates: \((− \ 1, 6), (− \ 2,5)\), and \((5,8)\). If triangle ABC is reflected over the \(y-\)axis, what are the coordinates of the new image? |
| (A) |
\((− \ 1, − \ 6), (− \ 2, − \ 5), (5, − \ 8)\) |
| (B) |
\((− \ 1,6), (− \ 2,5), (5,8)\) |
| (C) |
\((1,6), (2,5), (5,8)\) |
| (D) |
\((− \ 1, − \ 6), (− \ 2, − \ 5), (− \ 5, − \ 8)\) |
| (E) |
\((1,6), (2,5), (− \ 5,8)\) |
|
| 34- |
A cruise line ship left Port A and traveled \(80\) miles due west and then \(150\) miles due north. At this point, what is the shortest distance from the cruise to port A? |
| (A) |
\(120\) miles |
| (B) |
\(80\) miles |
| (C) |
\(150\) miles |
| (D) |
\(240\) miles |
| (E) |
\(170\) miles |
| 35- |
If the ratio of \(2 \ a\) to \(3 \ b\) is \(\frac{1}{15}\), what is the ratio of \(a\) to \(b\)? |
| (A) |
\(\frac{1}{10}\) |
| (B) |
\(\frac{1}{15}\) |
| (C) |
\(\frac{1}{25}\) |
| (D) |
\(10\) |
| (E) |
\(15\) |
| 36- |
Two-kilograms apple and four-kilograms orange cost \($25.4\). If one-kilogram apple costs \($4.2\) how much does one-kilogram orange cost? |
| (A) |
\($6\) |
| (B) |
\($5.5\) |
| (C) |
\($5\) |
| (D) |
\($4.5\) |
| (E) |
\($4\) |
| 37- |
Tickets to a movie cost \($12.50\) for adults and \($7.50\) for students. A group of \(12\) friends purchased tickets for \($125\). How many adults tickets did they buy? |
| (A) |
\(3\) |
| (B) |
\(4\) |
| (C) |
\(5\) |
| (D) |
\(6\) |
| (E) |
\(7\) |
| 38- |
If A \(=\begin{bmatrix}- \ 1 & 3 \\1 & - \ 3 \end{bmatrix}\) and B \(=\begin{bmatrix}2 & 1 \\- \ 2 & 2 \end{bmatrix}\) then \(2\) A \(-\) B \(=\)? |
| (A) |
\(\begin{bmatrix}4&5\\ 4&-\ 6\end{bmatrix}\) |
| (B) |
\(\begin{bmatrix}4&6\\ - \ 4&-\ 6\end{bmatrix}\) |
| (C) |
\(\begin{bmatrix}-\ 4&3\\ 2&-\ 6\end{bmatrix}\) |
| (D) |
\(\begin{bmatrix}-\ 4&- \ 8\\ 2&-\ 6\end{bmatrix}\) |
| (E) |
\(\begin{bmatrix}-\ 4&5\\ 4&-\ 8\end{bmatrix}\) |
| 39- |
\((x^5)^{\frac{3}{7}}\) equal to? |
| (A) |
\(x ^ {\frac{7}{17}}\) |
| (B) |
\(x ^ {\frac{7}{15}}\) |
| (C) |
\(x ^ {\frac{15}{7}}\) |
| (D) |
\(x ^ {\frac{17}{7}}\) |
| (E) |
\(x ^ {\frac{1}{7}}\) |
| 40- |
The width of a box is one third of its length. The height of the box is one third of its width. If the length of the box is \(45\) cm, what is the volume of the box? |
| (A) |
\(3,375\) |
| (B) |
\(375\) |
| (C) |
\(2,125\) |
| (D) |
\(2,625\) |
| (E) |
\(3,415\) |
| 41- |
What is the amplitude of the graph of the equation \(y \ - \ 1=2\) cos \(3 \ x\)?
(half the distance between the graph’s minimum and maximum \(y-\)values in standard \((x, y)\) coordinate plane is the amplitude of a graph.) |
| (A) |
\(1\) |
| (B) |
\(- \ 1\) |
| (C) |
\(- \ 2\) |
| (D) |
\(2\) |
| (E) |
\(0\) |
| 42- |
If one angle of a right triangle measures \(60^\circ\), what is the cos of the other acute angle? |
| (A) |
\(\frac{1}{2}\) |
| (B) |
\(\frac{\sqrt{2}}{2}\) |
| (C) |
\(\frac{\sqrt{2}}{3}\) |
| (D) |
\(\frac{\sqrt{3}}{2}\) |
| (E) |
\(1\) |
| 43- |
What is the difference in area between a \(8\) cm by \(4\) cm rectangle and a circle with diameter of \(10\) cm? \((π=3)\) |
| (A) |
\(32\) |
| (B) |
\(33\) |
| (C) |
\(51\) |
| (D) |
\(42\) |
| (E) |
\(43\) |
| 44- |
The average weight of \(15\) girls in a class is \(60\) kg and the average weight of \(37\) boys in the same class is \(64\) kg. What is the average weight of all the \(52\) students in that class? |
| (A) |
\(62.84 \) kg |
| (B) |
\(64.34\) kg |
| (C) |
\(58.90\) kg |
| (D) |
\(65.32\) kg |
| (E) |
\(71.23\) kg |
| 45- |
Between which two of the months shown was there a twenty percent decreased in the number of pants sold?
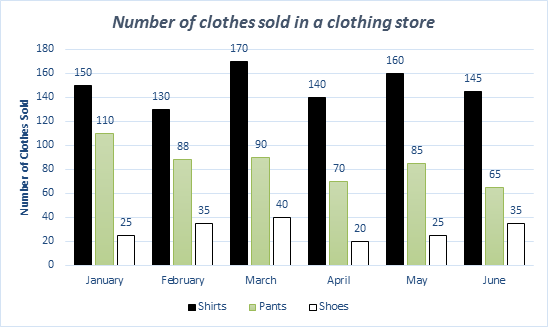 |
| (A) |
January and February |
| (B) |
February and March |
| (C) |
March and April |
| (D) |
April and May |
| (E) |
May and June |
| 46- |
During the six-month period shown, what is the median number of shirts and mean number of shoes per month?
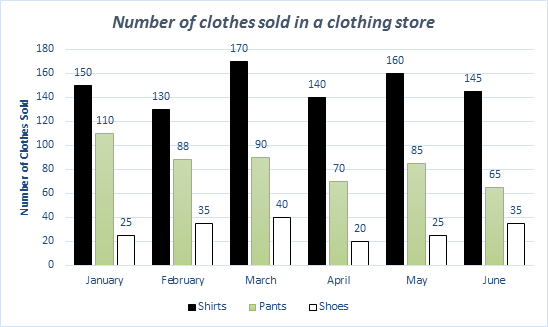 |
| (A) |
\(156.5, 30\) |
| (B) |
\(178.5, 29\) |
| (C) |
\(147.5, 30\) |
| (D) |
\(123.5, 31\) |
| (E) |
\(135.5, 32\) |
| 47- |
How many shoes need to be added in April until the ratio of pants to shoes in April equals to five-seventeenth of this ratio in May?
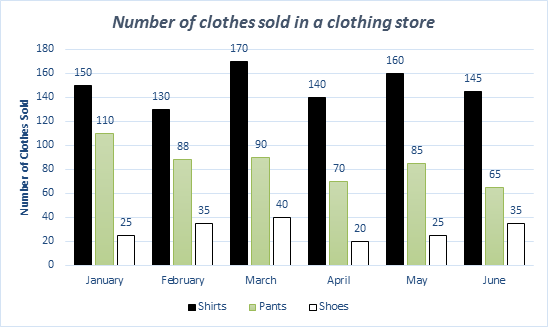 |
| (A) |
\(30\) |
| (B) |
\(40\) |
| (C) |
\(50\) |
| (D) |
\(60\) |
| (E) |
\(70\) |
| 48- |
What is the value of \(x\) in the following equation?
\(5^{ \ x}=3125\) |
| (A) |
\(4\) |
| (B) |
\(5\) |
| (C) |
\(6\) |
| (D) |
\(7\) |
| (E) |
\(3\) |
| 49- |
If \(x=5\), what is the value of \(y\) in the following equation?
\(3 \ y =\frac{2 \ x^3}{5} \ + \ 4\) |
| (A) |
\(17\) |
| (B) |
\(21\) |
| (C) |
\(32\) |
| (D) |
\(18\) |
| (E) |
\(12\) |
| 50- |
In the following figure, ABCD is a rectangle. If \(a=\sqrt{3}\), and \(b=3 \ a\), find the area of the shaded region. (the shaded region is a trapezoid)
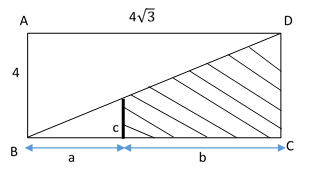 |
| (A) |
\(\frac{15 \ \sqrt{4}}{2}\) |
| (B) |
\(\frac{15 \ \sqrt{3}}{2}\) |
| (C) |
\(15 \ \sqrt{3}\) |
| (D) |
\( \sqrt{3}\) |
| (E) |
\( \frac{\sqrt{3}}{15}\) |
| 51- |
Which of the following is one solution of this equation?
\(x^2 \ + \ 2 \ x \ - \ 5=0\) |
| (A) |
\(\sqrt{2}\ -\ 1\) |
| (B) |
\(\sqrt{6}\ +\ 1\) |
| (C) |
\(\sqrt{12}\) |
| (D) |
\(\sqrt{2}\ +\ 1\) |
| (E) |
\(\sqrt{6}\ -\ 1\) |
| 52- |
A football team had \($23,000\) to spend on supplies. The team spent \($16,000\) on new balls. New sport shoes cost \($110\) each. Which of the following inequalities represent how many new shoes the team can purchase? |
| (A) |
\(110 \ x \ - \ 16,000 \ ≤ \ 23,000\) |
| (B) |
\(110 \ x \ + \ 16,000 \ ≤ \ 23,000\) |
| (C) |
\(110 \ - \ 16,000 \ x \ ≤ \ 23,000\) |
| (D) |
\(110 \ + \ 7,000 \ x \ \geq \ 24,000\) |
| (E) |
\(110 \ - \ 19,000 \ \ \geq \ 24,000 \ x\) |
| 53- |
If \(f(x)=3 \ x^2\ + \ 5\) and \(g(x)=- \ \frac{1}{x}\), what is the value of \(f(g(x))\)? |
| (A) |
\(\frac{3}{x^2} \ - \ 5\) |
| (B) |
\(\frac{3}{x^2} \ + \ 5\) |
| (C) |
\(\frac{2}{x^3} \ + \ 5\) |
| (D) |
\(\frac{3}{x^2} \) |
| (E) |
\(\frac{3}{x^2} \ - \ 2\) |
| 54- |
The length of a rectangle is \(4\) meters greater than \(3\) times its width. The perimeter of the rectangle is \(40\) meters. What is the area of the rectangle? |
| (A) |
\(45\) m\(^2\) |
| (B) |
\(52\) m\(^2\) |
| (C) |
\(64\) m\(^2\) |
| (D) |
\(69\) m\(^2\) |
| (E) |
\(73\) m\(^2\) |
| 55- |
What is the sum of prime numbers between \(20\) and \(40\)? |
| (A) |
\(120\) |
| (B) |
\(60\) |
| (C) |
\(92\) |
| (D) |
\(86\) |
| (E) |
\(112\) |
| 56- |
Simplify \(\frac{4 \ - \ 3 \ i}{- \ 4 \ i} \)? |
| (A) |
\(\frac{3}{4} \ -\ i\) |
| (B) |
\(\frac{1}{4} \ -\ i\) |
| (C) |
\( i\) |
| (D) |
\(\frac{3}{4} \ +\ i\) |
| (E) |
\(\frac{1}{4} \ +\ i\) |
| 57- |
What are the zeroes of the function \(f(x)=x^3 \ + \ 5 \ x^2 \ + \ 6 \ x\)? |
| (A) |
\(0, -\ 2 , 3\) |
| (B) |
\(0, 2 , 3\) |
| (C) |
\(1, 2 , 3\) |
| (D) |
\(1, 2 \) |
| (E) |
\(0, -\ 2 , -\ 3\) |
| 58- |
In the following figure, what is the perimeter of \(\triangle \)ABC if the area of \(\triangle \)ADC is \(12\)?
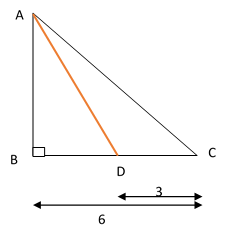 |
| (A) |
\(32.5\) |
| (B) |
\(15\) |
| (C) |
\(21\) |
| (D) |
\(24\) |
| (E) |
The answer cannot be determined from the information given |
| 59- |
A swimming pool holds \(5,000\) cubic feet of water. The swimming pool is \(20\) feet long and \(20\) feet wide. How deep is the swimming pool? |
| (A) |
\(10\) feet |
| (B) |
\(8\) feet |
| (C) |
\(8.5\) feet |
| (D) |
\(12.5\) feet |
| (E) |
\(15.5\) feet |
| 60- |
If \(y=(- \ 5 \ x^4)^2\), which of the following expressions is equal to \(y\)? |
| (A) |
\( 25 \ x^6\) |
| (B) |
\( 25 \ x^8\) |
| (C) |
\( 5 \ x^8\) |
| (D) |
\( - \ 25 \ x^8\) |
| (E) |
\( 25 \ x^4\) |