ISEE UPPER LEVEL
Mathematics Practice Test 4
- 47 questions
- Total time for this section: 40 Minutes
- Calculators are not allowed at the test.
|
| 1- |
Ella (E) is \(6\) years older than her friend Ava (A) who is \(4\) years younger than her sister Sofia (S). If E, A and S denote their ages, which one of the following represents the given information? |
| (A) |
\(\begin{cases}E = 6 \ - \ A\\A = S \ + \ 4\end{cases}\) |
| (B) |
\(\begin{cases}E = 4 \ - \ A\\A = S \ - \ 2\end{cases}\) |
| (C) |
\(\begin{cases}A = 4 \ - \ E\\S = A \ - \ 2\end{cases}\) |
| (D) |
\(\begin{cases}E = 6 \ + \ A\\A = S \ – \ 4\end{cases}\) |
| 2- |
An angle is equal to one fourth of its supplement. What is the measure of that angle? |
| (A) |
\(36^\circ\) |
| (B) |
\(30^\circ\) |
| (C) |
\(25^\circ\) |
| (D) |
\(39^\circ\) |
| 3- |
\(3\) less than twice a positive integer is \(91\). What is the integer? |
| (A) |
\(44\) |
| (B) |
\(45\) |
| (C) |
\(47\) |
| (D) |
\(49\) |
| 4- |
The cost, in thousands of dollars, of producing \(x\) thousands of textbooks is:
\(C(x)=x^2 \ - \ 4 \ x\).
The revenue, also in thousands of dollars, is \(R(x)=30 \ x\).
find the profit or loss if \(30\) textbooks are produced. (profit \(=\) revenue \(–\) cost) |
| (A) |
\($120\) profit |
| (B) |
\($240\) profit |
| (C) |
\($130\) loss |
| (D) |
\($180\) loss |
| 5- |
\(\frac{1}{4 \ b^2} \ + \ \frac{1}{4 \ b} = \frac{1}{b^2}\), then \(b =\)? |
| (A) |
\(3\) |
| (B) |
\(\frac{2}{7}\) |
| (C) |
\(- \ \frac{15}{17}\) |
| (D) |
\(- \ 3\) |
| 6- |
Simplify \(4 \ x^2 \ y^3 \ (3 \ x^2 \ y)^3=\) |
| (A) |
\( 100 \ x^6 \ y^6\) |
| (B) |
\( 108 \ x^8 \ y^6\) |
| (C) |
\( 54 \ x^5 \ y^3\) |
| (D) |
\(68 \ x^8 \ y^2\) |
| 7- |
\(\frac{|6 \ + \ x|}{2} \ ≤ \ 8\), then \(x =\)? |
| (A) |
\(– \ 28 \ ≤ \ x \ ≤ \ 12\) |
| (B) |
\(– \ 22 \ ≤ \ x \ ≤ \ 10\) |
| (C) |
\(– \ 24 \ ≤ \ x \ ≤ \ 15\) |
| (D) |
\(– \ 18\ ≤ \ x \ ≤ \ 18\) |
| 8- |
Which of the following points lies on the line \(2 \ x \ + \ 5 \ y=12\)? |
| (A) |
\((2, 1)\) |
| (B) |
\((– \ 1, 3)\) |
| (C) |
\((– \ 2, 2)\) |
| (D) |
\((2, 2)\) |
| 9- |
\(1.3\) is what percent of \(13\)? |
| (A) |
\(4\) |
| (B) |
\(10\) |
| (C) |
\(5\) |
| (D) |
\(12\) |
| 10- |
Write \(674\) in expanded form, using exponents. |
| (A) |
\((6 \ × \ 10^3) \ + \ (7 \ × \ 10^2) \ + \ (4 \ × \ 10) \) |
| (B) |
\((6 \ × \ 10^2) \ + \ (7 \ × \ 10^1) \ – \ 4 \) |
| (C) |
\((6 \ × \ 10^2) \ + \ (7 \ × \ 10^1) \ + \ 4\) |
| (D) |
\((6 \ × \ 10^1) \ + \ (7 \ × \ 10^1) \ + \ 4\) |
| 11- |
What is the area of an isosceles right triangle that has one leg that measures \(4\) cm? |
| (A) |
\(4\) cm\(^2\) |
| (B) |
\(8\) cm\(^2\) |
| (C) |
\(12\) cm\(^2\) |
| (D) |
\(16\) cm\(^2\) |
| 12- |
Right triangle ABC has two legs of lengths \(5\) cm (AB) and \(12\) cm (AC). What is the length of the third side (BC)? |
| (A) |
\(12\) cm |
| (B) |
\(11\) cm |
| (C) |
\(13\) cm |
| (D) |
\(15\) cm |
| 13- |
A circle has a diameter of \(12\) inches. What is its approximate circumference? |
| (A) |
\(44.24\) |
| (B) |
\(64.91\) |
| (C) |
\(34.28\) |
| (D) |
\(37.68\) |
| 14- |
A company pays its writer \($5\) for every \(200\) words written. How much will a writer earn for an article with \(1,100\) words? |
| (A) |
\($22.5\) |
| (B) |
\($21.7\) |
| (C) |
\($27.5\) |
| (D) |
\($30.6\) |
| 15- |
Which is the longest time? |
| (A) |
\(23\) hours |
| (B) |
\(1610\) minutes |
| (C) |
\(1\) days |
| (D) |
\(3,900\) |
| 16- |
The equation of a line is given as : \(y = 6 \ , x \ – \ 2\). Which of the following points lie on the line? |
| 17- |
\(85.23 \ ÷ \ 0.03 =\)? |
| (A) |
\(1,931\) |
| (B) |
\(2,969\) |
| (C) |
\(2,841\) |
| (D) |
\(2,691\) |
| 18- |
The drivers at G & G trucking must report the mileage on their trucks each week. The mileage reading of Ed’s vehicle was \(42,687\) at the beginning of one week, and \(47,353\) at the end of the same week. What was the total number of miles driven by Ed that week? |
| (A) |
\(489\) Miles |
| (B) |
\(723\) Miles |
| (C) |
\(692\) Miles |
| (D) |
\(666\) Miles |
| 19- |
A circular logo is enlarged to fit the lid of a jar. The new diameter is \(25\%\) larger than the original. By what percentage has the area of the logo increased? |
| (A) |
\(69\%\) |
| (B) |
\(54\%\) |
| (C) |
\(76\%\) |
| (D) |
\(39\%\) |
| 20- |
What is the area of an isosceles right triangle that has one leg that measures \(8\) cm? |
| (A) |
\(32\) cm\(^2\) |
| (B) |
\(64\) cm\(^2\) |
| (C) |
\(53\) cm\(^2\) |
| (D) |
\(24\) cm\(^2\) |
| 21- |
If \(x \ + \ y = 24\), what is the value of \(4 \ x \ + \ 4 \ y\)? |
| (A) |
\(76\) |
| (B) |
\(80\) |
| (C) |
\(100\) |
| (D) |
\(96\) |
| 22- |
What’s the area of the non-shaded part of the following figure?
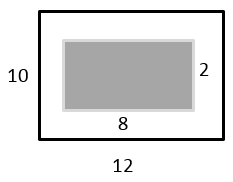 |
| (A) |
\(104\) |
| (B) |
\(78\) |
| (C) |
\(120\) |
| (D) |
\(112\) |
| 23- |
What’s the reciprocal of \(\frac{x^3}{16}\)? |
| (A) |
\(\frac{16}{x^3}\) |
| (B) |
\(\frac{16}{x^3} \ - \ 1\) |
| (C) |
\(\frac{x^3}{16} \ - \ 1\) |
| (D) |
\(\frac{x^3}{16} \ + \ 1\) |
| 24- |
Given that \(x = 0.5\) and \(y = 3\), what is the value of \(2 \ x^2 \ (y \ + \ 8)\)? |
| (A) |
\(5.5\) |
| (B) |
\(7.2\) |
| (C) |
\(11.4\) |
| (D) |
\(8.9\) |
| 25- |
Mario loaned Jett \($2,500\) at a yearly interest rate of \(4\%\). After two year what is the interest owned on this loan? |
| (A) |
\($245\) |
| (B) |
\($195\) |
| (C) |
\($185\) |
| (D) |
\($200\) |
| 26- |
Which equation represents the statement Two plus the sum of the squares of \(w\) and \(x\) is \(25\). |
| (A) |
\( 2 \ (w^2 \ - \ x) = 25\) |
| (B) |
\( 2 \ (w^2 \ + \ x) = 25\) |
| (C) |
\( 25 \ (w^2 \ + \ x) = 2\) |
| (D) |
\( 2 \ (w \ + \ x) = 25\) |
$24.99 $16.99
32% Off*
The Ultimate Step by Step Guide to Preparing for the ISEE Upper Level Math Test
|
| 27- |
\(29\) hr. \(21\) min
\(23\) hr. \(44\) min
_________________
|
| (A) |
\(5\) hr. \(37\) min |
| (B) |
\(6\) hr. \(37\) min |
| (C) |
\(6\) hr. \(13\) min |
| (D) |
\(5\) hr. \(13\) min |
| 28- |
A bread recipe calls for \(4 \ \frac{1}{2}\) cups of flour. If you only have \(5 \frac{4}{3}\) cups, how much more flour is needed? |
| (A) |
\( \frac{ 5}{4}\) |
| (B) |
\(- \ \frac{ 5}{4}\) |
| (C) |
\(- \ \frac{ 1}{2}\) |
| (D) |
\(1\) |
| 29- |
Which of the following is a factor of both \(x^2 \ - \ 2 \ x \ - \ 8\) and \(x^2 \ - \ 6 \ x \ + \ 8\)? |
| (A) |
\((x \ – \ 2)\) |
| (B) |
\((x \ + \ 2)\) |
| (C) |
\((x \ + \ 4)\) |
| (D) |
\((x \ - \ 4)\) |
| 30- |
What is the solution of the following system of equations?
\(\begin{cases}- \ 2 \ x \ - \ 3 \ y =\ - \ 12\\4 \ x\ + \ y= 25\end{cases}\) |
| (A) |
\((4, 2)\) |
| (B) |
\((7, 2)\) |
| (C) |
\((6, 1)\) |
| (D) |
\((5, 3)\) |
| 31- |
Ellis just got hired for on-the-road sales and will travel about \(1,200\) miles a week during an \(60-\)hour work week. If the time spent traveling is \(\frac{2}{3}\) of his week, how many hours a week will he be on the road? |
| (A) |
Ellis spends about \(48\) hours of his \(60-\)hour work week on the road. |
| (B) |
Ellis spends about \(40\) hours of his \(60-\)hour work week on the road. |
| (C) |
Ellis spends about \(44\) hours of his \(60-\)hour work week on the road. |
| (D) |
Ellis spends about \(42\) hours of his \(60-\)hour work week on the road. |
| 32- |
\(\frac{12}{27}\) is equal to: |
| (A) |
\(0.444\)... |
| (B) |
\(0.25\) |
| (C) |
\(0.40\) |
| (D) |
\(0.38\) |
| 33- |
Find the perimeter of a rectangle with the dimensions \(49 \ × \ 28\). |
| (A) |
\(132\) |
| (B) |
\(281\) |
| (C) |
\(154\) |
| (D) |
\(164\) |
| 34- |
In a school, the ratio of number of boys to girls is \(5:9\). If the number of boys is \(235\), what is the total number of students in the school? |
| (A) |
\(780\) |
| (B) |
\(658\) |
| (C) |
\(568\) |
| (D) |
\(865\) |
| 35- |
A car uses \(12\) gallons of gas to travel \(240\) miles. How many miles per gallon does the car get? |
| (A) |
\(20\) |
| (B) |
\(12\) |
| (C) |
\(30\) |
| (D) |
\(25\) |
| 36- |
How many square feet of tile is needed for a \(12\) foot \(x \ 12\) foot room? |
| (A) |
\(256\) square feet |
| (B) |
\(144\) square feet |
| (C) |
\(169\) square feet |
| (D) |
\(218\) square feet |
| 37- |
If \(x\) is \(38\%\) percent of \(740\), what is \(x\)? |
| (A) |
\(270.5\) |
| (B) |
\(240.1\) |
| (C) |
\(281.2\) |
| (D) |
\(269.7\) |
| 38- |
Karen is \(6\) years older than her sister Michelle, and Michelle is \(4\) years younger than her brother David. If the sum of their ages is \(67\), how old is Michelle? |
| (A) |
\(21\) |
| (B) |
\(19\) |
| (C) |
\(25\) |
| (D) |
\(17\) |
| 39- |
A tree \(24\) feet tall casts a shadow \(8\) feet long. Jack is \(6\) feet tall. How long is Jack’s shadow? |
| (A) |
\(3\) ft. |
| (B) |
\(5\) ft. |
| (C) |
\(2\) ft. |
| (D) |
\(\frac{1}{2}\) ft. |
| 40- |
Calculate the area of a parallelogram with a base of \(3\) feet and height of \(4.2\) feet. |
| (A) |
\(10.2\) square feet |
| (B) |
\(15.5\) square feet |
| (C) |
\(18.6\) square feet |
| (D) |
\(12.6\) square feet |
| 41- |
What is the result of the expression?
\(\begin{bmatrix}2 & 6 \\- \ 1 & - \ 2\\- \ 5 & - \ 4 \end{bmatrix} \ + \ \begin{bmatrix}0 & - \ 6 \\1 & 0\\2 & 7 \end{bmatrix}=\) |
| (A) |
\(\ \begin{bmatrix}2 & 0\\0 & - \ 2\\- \ 3 & 3 \end{bmatrix}\) |
| (B) |
\(\ \begin{bmatrix}0 & 2\\0 & - \ 2\\3 & - \ 3 \end{bmatrix}\) |
| (C) |
\(\ \begin{bmatrix}1 & 3\\0 & - \ 3\\2 & - \ 2 \end{bmatrix}\) |
| (D) |
\(\ \begin{bmatrix}- \ 1 & 0\\2 & - \ 3\\2 & 0 \end{bmatrix}\) |
| 42- |
If \(x∎y=\sqrt{x^2 \ + \ y}\), what is the value of \(7∎15\)? |
| (A) |
\(\sqrt{63}\) |
| (B) |
\(8\) |
| (C) |
\(6\) |
| (D) |
\(9\) |
| 43- |
A shirt costing \($150\) is discounted \(15\%\). After a month, the shirt is discounted another \(15\%\). Which of the following expressions can be used to find the selling price of the shirt? |
| (A) |
\((150) \ (0.85)\) |
| (B) |
\((150) \ (0.85) \ - \ (0.70)\) |
| (C) |
\((150) \ (0.85) \ - \ (150) \ (0.70)\) |
| (D) |
\((150) \ (0.85) \ (0.70)\) |
| 44- |
The average weight of \(21\) girls in a class is \(65\) kg and the average weight of \(30\) boys in the same class is \(72\) kg. What is the average weight of all the \(51\) students in that class? |
| (A) |
\(69.11\) kg |
| (B) |
\(73\) kg |
| (C) |
\(65.32\) kg |
| (D) |
\(70\) kg |
| 45- |
There are three equal tanks of water. If \(\frac{3}{4}\) of a tank contains \(320\) liters of water, what is the capacity of the two tanks of water together? |
| (A) |
\(450\) Liters |
| (B) |
\(240\) Liters |
| (C) |
\(720\) Liters |
| (D) |
\(480\) Liters |
| 46- |
\((2 \ x \ + \ 6) \ (- \ x \ + \ 2) =\) |
| (A) |
\( 2 \ x^2 \ + \ 2 \ x \ - \ 12 \) |
| (B) |
\( x^2 \ + \ 4 \ x \ - \ 4 \) |
| (C) |
\(- \ 2 \ x^2 \ - \ 2 \ x \ + \ 12 \) |
| (D) |
\(- \ 2 \ x^2 \ + \ 2 \ x \ - \ 6\) |
| 47- |
What is the area of the shaded region if the diameter of the bigger circle is \(18\) inches and the diameter of the smaller circle is \(8\) inches?
 |
| (A) |
\( 49 \ π\) |
| (B) |
\( 81 \ π\) |
| (C) |
\( 72 \ π\) |
| (D) |
\( 65 \ π\) |