ACCUPLACER Mathematics Practice Test 3
(Non–Calculator) 2 Sections – 40 questions Total time for two sections: No Time Limit You may not use a calculator on this section.
|
| Arithmetic and Elementary Algebra |
| 1- |
Which of the following is a factor of both \( x^2 \ -\ 9 \ x \ + \ 18\) and \( x^2 \ – \ 7 \ x \ +\ 6\) ? |
| (A) |
(\(x \ + \ 6\)) |
| (B) |
(\(x \ + \ 3\)) |
| (C) |
(\(x \ - \ 6\)) |
| (D) |
(\(x \ - \ 1\)) |
| 2- |
What is the area of an isosceles right triangle that has one leg that measures \( 6 \) cm? |
| (A) |
\(18\) cm\(^2\) |
| (B) |
\(36\) cm\(^2\) |
| (C) |
\(9\) cm\(^2\) |
| (D) |
\(20\) cm\(^2\) |
| 3- |
If two angles in a triangle measure \( 46 \) degrees and \(72\) degrees, what is the value of the third angle? |
| (A) |
\(64\) degrees |
| (B) |
\(56\) degrees |
| (C) |
\(46\) degrees |
| (D) |
\(62\) degrees |
| 4- |
Which of the following expressions is equivalent to \( 15 \ – \ \frac{4}{3} \ x \ \leq \ 1\) |
| (A) |
\(x \leq \ – \ 10.5 \) |
| (B) |
\(x \geq \ 10.5 \) |
| (C) |
\(x \geq \ 12 \) |
| (D) |
\(x \leq \ 12 \) |
| 5- |
\( \frac{1}{2\ b^2} \ + \ \frac{1}{ b} \ = \ \frac{1}{b^2} \) , then \( b = \) ? |
| (A) |
\(\frac{1}{2}\) |
| (B) |
\(- \ \frac{1}{2}\) |
| (C) |
\(- \ \frac{3}{2}\) |
| (D) |
\( \frac{3}{2}\) |
| 6- |
\( 7^{\frac{6}{5}} \ × \ 7^{\frac{4}{5}} \)= |
| (A) |
\(7^5\) |
| (B) |
\(7^3\) |
| (C) |
\(7^4\) |
| (D) |
\(7^2\) |
| 7- |
If \( a^7 \ + \ c^7 \ = \ c^7 \ + \ b^7\) , then \( a \ =\) ? |
| (A) |
\( c\) |
| (B) |
\( b\) |
| (C) |
\( b^{4} \ – \ a^{4} \) |
| (D) |
\( b^{3} \ – \ a^{4} \) |
| 8- |
What is \(178.4786 \) rounded to the nearest hundredth? |
| (A) |
\(178.47\) |
| (B) |
\(178.50\) |
| (C) |
\(178.46\) |
| (D) |
\(178.48\) |
| 9- |
The equation of a line is given as: \( y \ = \ 6 \ x \ – \ 1\) . Which of the following points does not lie on the line? |
| (A) |
\((1,2)\) |
| (B) |
\((- \ 2 ,- \ 13 )\) |
| (C) |
\((3 , 17 )\) |
| (D) |
\((1, 5 )\) |
| 10- |
A soccer team played \( 210 \) games and won \( 60 \) percent of them. How many games did the team win? |
| (A) |
\(125\) |
| (B) |
\(124\) |
| (C) |
\(123\) |
| (D) |
\(126\) |
| 11- |
The sum of three numbers is \( 64 \) . If another number is added to these three numbers, the average of the four numbers is \( 28 \) .
What is the fourth number? |
| (A) |
\(58\) |
| (B) |
\(48\) |
| (C) |
\(38\) |
| (D) |
\(28\) |
| 12- |
Line m passes through the point \( (2, 3) \) . Which of the following CANNOT be the equation of line m? |
| (A) |
\(y = 1 \ - \ x\) |
| (B) |
\( y = 3 \) |
| (C) |
\( x = 2 \) |
| (D) |
\( y = x \ + \ 1\) |
| 13- |
If \( a = 9 \) what’s the value of \( 3 \ a^{2} \ + \ 7 \ a \ - \ 8 \)? |
| (A) |
\(296\) |
| (B) |
\(298\) |
| (C) |
\(300\) |
| (D) |
\(295\) |
| 14- |
David owed \( $7216 \) . After making \( 32 \) payments of \( $115 \) each , how much did he have left to pay? |
| (A) |
\($3,526\) |
| (B) |
\($3,525\) |
| (C) |
\($3,515\) |
| (D) |
\($3,536\) |
| 15- |
\( (q^{3}) \ . \ (q^{3}) \ =\) ? |
| (A) |
\( q^3\) |
| (B) |
\( q^9\) |
| (C) |
\( q^6\) |
| (D) |
\( q^5\) |
$24.99 $13.99
44% Off*
The Ultimate Step by Step Guide to Preparing for the Accuplacer Math Test
|
| 16- |
\( x^{2} \ – \ 64 \ = \ 0 \) , \( x \) could equal to: |
| (A) |
\(8\) |
| (B) |
\(9\) |
| (C) |
\(6\) |
| (D) |
\(5\) |
| 17- |
\( (x \ + \ 2) \ (x \ - \ 6) \ =\) |
| (A) |
\(x^{2} \ - \ 4 \ x \ + \ 12\) |
| (B) |
\(x^{2} \ + \ 4 \ x \ + \ 12\) |
| (C) |
\(x^{2} \ - \ 4 \ x \ - \ 12\) |
| (D) |
\(x^{2} \ + \ 4 \ x \ - \ 12\) |
| 18- |
If \(x\) is a positive integer divisible by \(9\), and \( x \ < \ 81 \) , what is the greatest possible value of \( x \) ? |
| (A) |
\(54\) |
| (B) |
\(72\) |
| (C) |
\(36\) |
| (D) |
\(45\) |
| 19- |
If \( 7.5 \ < \ x \ ≤ \ 11.0 \) , then \( x\) cannot be equal to: |
| (A) |
\(7.5\) |
| (B) |
\(11.0\) |
| (C) |
\(9.2\) |
| (D) |
\(10.1\) |
| 20- |
If \(a = 6\) , what is the value of b in this equation?
\(b = \ \frac{a^{2}}{3} \ + \ 4\) |
| (A) |
\(14\) |
| (B) |
\(8\) |
| (C) |
\(16\) |
| (D) |
\(13\) |
| College–Level Mathematics |
| 21- |
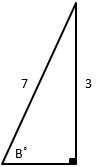
Suppose a triangle has the dimensions indicated below:
Then Sin \(B =\) ?
 |
| (A) |
\(\frac{3}{4}\) |
| (B) |
\(\frac{7}{3}\) |
| (C) |
\(\frac{3}{6}\) |
| (D) |
\(\frac{3}{7}\) |
| 22- |
A number is chosen at random from \(1\) to \( 50 \) . Find the probability of not selecting a composite number. |
| (A) |
\(\frac{8}{25}\) |
| (B) |
\(\frac{6}{25}\) |
| (C) |
\(\frac{5}{25}\) |
| (D) |
\(\frac{4}{25}\) |
| 23- |
The cost, in thousands of dollars, of producing \(x \) thousands of textbooks is \(C (x) \ = \ x^{2} \ + \ 10 \ x \ + \ 30\) . The revenue, also in thousands of dollars, is \(R (x) = 3 \ x \). Find the profit or loss if \( 2,000 \) textbooks are produced. (profit \(=\) revenue \(–\) cost) |
| (A) |
\($22,000\) profit |
| (B) |
\($22,000\) loss |
| (C) |
\($28,000\) loss |
| (D) |
\($28,000\) profit |
| 24- |
Find the slope – intercept form of the graph \( 5 \ x \ – \ 9 \ y \ = \ – \ 16\) |
| (A) |
\(\ y = \frac{5}{9} \ x \ + \ \frac{16}{9} \) |
| (B) |
\( - \ 9 \ y = - \ 5 \ x \ - \ 16 \) |
| (C) |
\(y = - \ 5 \ x \ - \ 16 \) |
| (D) |
\(y = 5 \ x \ - \ 16 \) |
| 25- |
Solve \( e^{(x \ + \ 4 )} = 32 \) |
| (A) |
\(ln \ (32) \ + \ 4\) |
| (B) |
\(ln \ (32) \ + \ 2\) |
| (C) |
\(ln \ (32) \ - \ 4\) |
| (D) |
\(ln \ (32) \ - \ 2\) |
| 26- |
If tan \(\theta \ = \ \frac{8}{15} \) and sin \(\theta \ > \ 0 \), then cos \(\theta \ =\) ? |
| (A) |
\(\frac{17}{15} \) |
| (B) |
\(\frac{15}{17} \) |
| (C) |
\(\frac{8}{17} \) |
| (D) |
\(\frac{17}{8} \) |
| 27- |
Michael (M ) is \( 3\) years older than her friend Alex (A) who is \( 5\) years younger than her sister John (J ). If M , A and J denote their ages, which one of the following represents the given information? |
| (A) |
\(\begin{cases}M \ = \ A \ + \ 3\\ J \ = \ A \ - \ 5\end{cases}\) |
| (B) |
\(\begin{cases}M = A \ - \ 3 \\ A = J \ - \ 5\end{cases}\) |
| (C) |
\(\begin{cases}M = 3 \ + \ A \\ A = 5 \ - \ J\end{cases}\) |
| (D) |
\(\begin{cases}M = 3 \ + \ A \\ A = J \ - \ 5\end{cases}\) |
| 28- |
Solve the equation: \( log_2 \ (x \ + \ 6) \ – \ log_2(x \ - \ 2) \ = \ 1\) |
| (A) |
\( - \ 2\) |
| (B) |
\( - \ 10\) |
| (C) |
\(2\) |
| (D) |
\(10\) |
| 29- |
From \(9\) students in an algebra class, a group of \( 3 \) students will be chosen to work on a group project. How many different groups of \(4 \) students can be chosen? |
| (A) |
\(72\) |
| (B) |
\(21\) |
| (C) |
\(36\) |
| (D) |
\(48\) |
| 30- |
What is the domain of the following function?
\( f (x) \ = \ \sqrt{(x \ - \ 6 )} \ + \ 4\) |
| (A) |
\(x \ ≥ - \ 6 \) |
| (B) |
\(x \leq - \ 6 \) |
| (C) |
\(x \leq 6 \) |
| (D) |
\(x \ \geq 6 \) |
| 31- |
Which of the following point is the solution of the system of equations?
\( \begin{cases}12\ x \ + \ 4 \ y \ = \ 32 \\6 \ x \ - \ 2 \ y = 8\end{cases} \) |
| (A) |
\( (- \ 2, 2) \) |
| (B) |
\( ( 2, 2) \) |
| (C) |
\( ( 2, - \ 2) \) |
| (D) |
\( (- \ 2, - \ 2) \) |
| 32- |
if \( f (x) \ = \ \frac{(4 \ x \ - \ 1 )}{2 } \) and \( f ^{ \ – \ 1}(x) \) , is the inverse of \( f (x) \), what is the value of \( f ^{ \ – \ 1}(3) \) ? |
| (A) |
\(\frac{5}{4}\) |
| (B) |
\(\frac{3}{4}\) |
| (C) |
\(\frac{7}{4}\) |
| (D) |
\(\frac{9}{4}\) |
| 33- |
If \( f (x) \ = \ 7 \ - \ x \) and \(g (x) \ = \ – \ x^2 \ – \ 3 \ – \ 5 \ x\) , then find \((g \ + \ f) (x)\)? |
| (A) |
\(– \ x^2 \ – \ 6 \ x \ + \ 4\) |
| (B) |
\(– \ x^2 \ – \ 6 \ x \ - \ 4\) |
| (C) |
\(– \ x^2 \ + \ 6 \ x \ - \ 4\) |
| (D) |
\(– \ x^2 \ + \ 6 \ x \ + \ 4\) |
| 34- |
Find the Center and Radius of the graph \( (x \ - \ 4)^{2} \ + \ (y \ + \ 7)^{2} \ = \ 18 \) ? |
| (A) |
\(( 4 , 7 )\), \(3 \ \sqrt{2} \) |
| (B) |
\(( 4 , 7 )\), \(2 \ \sqrt{3} \) |
| (C) |
\((- \ 4 , 7 )\), \(3 \ \sqrt{2} \) |
| (D) |
\((4 ,- \ 7 )\), \(3 \ \sqrt{2} \) |
| 35- |
Which of the following lines is parallel to the graph of \( y \ = \ 4 \ x \) ? |
| (A) |
\(4 \ x \ + \ y \ = \ 4\) |
| (B) |
\(4 \ x \ - \ y \ = \ 4\) |
| (C) |
\(2 \ x \ - \ y \ = \ 4\) |
| (D) |
\(2 \ x \ - \ y \ = \ 2\) |
| 36- |
\( \frac{| \ 6 \ + \ x \ |}{8} \ ≤ \ 3 \) , then \( x \) =? |
| (A) |
\( - \ 30 \ ≤ \ x \ ≤ \ - \ 18 \) |
| (B) |
\( 30 \ ≤ \ x \ ≤ \ 18 \) |
| (C) |
\( - \ 30 \ ≤ \ x \ ≤ \ 18 \) |
| (D) |
\( - \ 18 \ ≤ \ x \ ≤ \ 18 \) |
| 37- |
Simplify \( \frac{(4 \ + \ i)}{2\ - \ 3 \ i} \) |
| (A) |
\( \frac{5}{13} \ - \ i \ \frac{14}{13}\) |
| (B) |
\( \frac{5}{13} \ +\ i \ \frac{14}{13}\) |
| (C) |
\( - \ \frac{5}{13} \ +\ i \ \frac{14}{13}\) |
| (D) |
\( - \ \frac{5}{13} \ - \ i \ \frac{14}{13}\) |
| 38- |
tan \(( \frac{π}{3}) \ =\) ? |
| (A) |
\(- \ \sqrt3\) |
| (B) |
\(- \ 3 \ \sqrt3\) |
| (C) |
\(3 \ \sqrt3\) |
| (D) |
\( \sqrt3\) |
| 39- |
\( \frac{\sqrt{48 \ a^7 \ b^2}}{\sqrt{4 \ a^2 \ b^2}} \) =? |
| (A) |
\( 2 \ a\ \sqrt{3}\) |
| (B) |
\( 2 \ a^2\ \sqrt{3 \ a}\) |
| (C) |
\( 2 \ a^2\ \sqrt{3 \ b}\) |
| (D) |
\( 2 \ a\ \sqrt{3 \ b}\) |
| 40- |
Find the inverse function of \( f (x) \ = \ \frac{(x \ - \ 4 )}{8} \) |
| (A) |
\(4 \ (2 \ x \ - \ 1)\) |
| (B) |
\(4 \ (2 \ x \ + \ 1)\) |
| (C) |
\( (2 \ x \ + \ 1)\) |
| (D) |
\( (2 \ x \ - \ 1)\) |