|
ISEE Middle Level
Practice Test 3
Quantitative Reasoning
- 37 questions
- Total time for this section: 35 Minutes
- Calculators are not allowed at the test.
|
| 1- |
Solve. \(\frac{- \ 45 \ × \ 0.2}{5}\) |
| (A) |
\(- \ \frac{9}{5}\) |
| (B) |
\(- \ \frac{7}{5}\) |
| (C) |
\(\frac{4}{5}\) |
| (D) |
\(- \ 2\) |
| 2- |
Jim purchased a table for \(10\%\) off and saved \($25\). What was the original price of the table? |
| (A) |
\($250\) |
| (B) |
\($240\) |
| (C) |
\($220\) |
| (D) |
\($230\) |
| 3- |
The area of a circle is \(49 \ π\) in\(^2\). What is the circumference of the circle? |
| (A) |
\( 16 \ π\) |
| (B) |
\( 12 \ π\) |
| (C) |
\( 14 \ π\) |
| (D) |
\( 18 \ π\) |
| 4- |
What is the value of \(x\) in the following equation? \(9^x=729\) |
| (A) |
\(2\) |
| (B) |
\(3\) |
| (C) |
\(4\) |
| (D) |
\(5\) |
| 5- |
A \($40\) shirt now selling for \($30\) is discounted by what percent? |
| (A) |
\(25\%\) |
| (B) |
\(30\%\) |
| (C) |
\(35\%\) |
| (D) |
\(20\%\) |
| 6- |
Which of the following shows the numbers in descending order? |
| (A) |
\(\frac{3}{8}, \frac{1}{8}, \frac{2}{5}, \frac{1}{2}\) |
| (B) |
\(\frac{1}{8}, \frac{3}{8}, \frac{2}{5}, \frac{1}{2}\) |
| (C) |
\(\frac{1}{2}, \frac{3}{8}, \frac{2}{5}, \frac{1}{8}\) |
| (D) |
\(\frac{2}{5}, \frac{3}{8}, \frac{1}{8}, \frac{1}{2}\) |
| 7- |
The score of Emma was half as that of Ava and the score of Mia was twice that of Ava. If the score of Mia was \(30\), what is the score of Emma? |
| (A) |
\(5\) |
| (B) |
\(15\) |
| (C) |
\(10\) |
| (D) |
\(20\) |
| 8- |
If \(f=2 \ x \ - \ 6 \ y\) and \(g=x \ + \ 2 \ y\), what is \(2 \ f \ + \ g\)? |
| (A) |
\(5 \ x \ + \ 20 \ y\) |
| (B) |
\(2 \ x \ + \ 10 \ y\) |
| (C) |
\(5 \ x \ - \ 10 \ y\) |
| (D) |
\(- \ 5 \ x \ + \ 10 \ y\) |
| 9- |
\(712,232,691 \ × \ 0.001\)? |
| (A) |
\(71,223.2691 \) |
| (B) |
\(7,122,326.91 \) |
| (C) |
\(712,232.691 \) |
| (D) |
\(7,122.32691 \) |
| 10- |
one third of \(12\) is equal to \(\frac{1}{4}\) of what number? |
| (A) |
\(16\) |
| (B) |
\(12\) |
| (C) |
\(8\) |
| (D) |
\(24\) |
| 11- |
What is the mean in the following set of numbers?
\(7,15,26,32,48,63,100,121\) |
| (A) |
\(51\) |
| (B) |
\(51.5\) |
| (C) |
\(54.5\) |
| (D) |
\(54\) |
| 12- |
Round off the result of \(1.18 \ × \ 6.3\) to the nearest tenth? |
| (A) |
\(7.40\) |
| (B) |
\(7.43\) |
| (C) |
\(7.44\) |
| (D) |
\(7.41\) |
| 13- |
Find \(\frac{1}{3} \) of \(\frac{5}{6}\) of \(360\)? |
| (A) |
\(150\) |
| (B) |
\(200\) |
| (C) |
\(250\) |
| (D) |
\(100\) |
| 14- |
What is the value of \(x\) in the following equation?
\(3 \ (x \ + \ 5) = 2 \ (x \ − \ 1) \ + \ 15\) |
| (A) |
\( - \ 2\) |
| (B) |
\( 2\) |
| (C) |
\(5\) |
| (D) |
\(3\) |
| 15- |
What is the value of \(x\) in the following figure?
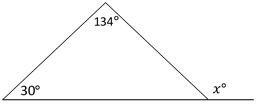 |
| (A) |
\(16^\circ\) |
| (B) |
\(132^\circ\) |
| (C) |
\(164^\circ\) |
| (D) |
\(150^\circ\) |
| 16- |
What is the value of \(x\) in the following figure?
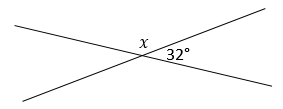 |
| (A) |
\(148^\circ\) |
| (B) |
\(152^\circ\) |
| (C) |
\(140^\circ\) |
| (D) |
\(125^\circ\) |
| 17- |
The ratio of boys and girls in a class is \(2:5\). If there are \(49\) students in the class, how many more boys should be enrolled to make the ratio \(1:1\)? |
| (A) |
\(24\) |
| (B) |
\(21\) |
| (C) |
\(35\) |
| (D) |
\(18\) |
| 18- |
In five successive hours, a car travels \(38\) km, \(40\) km, \(54\) km, \(32\) km and \(61\) km. In the next five hours, it travels with an average speed of \(54\) km per hour. Find the total distance the car traveled in \(10\) hours. |
| (A) |
\(475\) km |
| (B) |
\(425\) km |
| (C) |
\(495\) km |
| (D) |
\(455\) km |
| 19- |
The price of a laptop is decreased by \(12\%\) to \($280\). What is its original price? |
| (A) |
\($200\) |
| (B) |
\($400\) |
| (C) |
\($300\) |
| (D) |
\($500\) |
| 20- |
A company pays its employee \($5,000\) plus \(5\%\) of all sales profit. If \(x\) is all sold profit, which of the following represents the employee’s revenue? |
| (A) |
\(0.5 \ x \ - \ 5,000\) |
| (B) |
\(- \ 0.05 \ x \ - \ 5,000\) |
| (C) |
\(0.05 \ x \ + \ 500\) |
| (D) |
\(0.05 \ x \ + \ 5,000\) |
| 21- |
The perimeter of the trapezoid below is \(45\). What is its area?
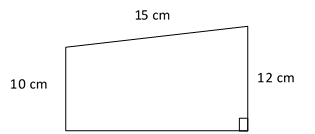 |
| (A) |
\(88\) cm\(^2\) |
| (B) |
\(82\) cm\(^2\) |
| (C) |
\(93\) cm\(^2\) |
| (D) |
\(79\) cm\(^2\) |
| 22- |
What is value of \(- \ 22 \ - \ (- \ 71)\)? |
| (A) |
\(29\) |
| (B) |
\(39\) |
| (C) |
\(49\) |
| (D) |
\(59\) |
| 23- |
Which of the following is a correct statement? |
| (A) |
\(\frac{3}{2} \ > \ 2.8\) |
| (B) |
\(10\%=\frac{1}{5}\) |
| (C) |
\(4 \ < \ \frac{3}{6}\) |
| (D) |
\(\frac{2}{5} \ > \ 0.3\) |
| 24- |
What is the area of a square whose diagonal is \(6\)? |
| (A) |
\(36\) |
| (B) |
\(30\) |
| (C) |
\(32\) |
| (D) |
\(38\) |
| 25- |
Car A use \(10-\)liter petrol per \(100\) kilometers; car B use \(6-\)liter petrol per \(100\) kilometers. If both cars drive \(350\) kilometers, how much more petrol does car A use? |
| (A) |
\(28\) |
| (B) |
\(14\) |
| (C) |
\(24\) |
| (D) |
\(12\) |
| 26- |
Using the information provided below, compare the quantity in column A to the quantity in Column B.
\( x^2 \ + \ 15 \ =\ 64\)
\(124 \ - \ 15 \ y\ =\ 49\)
| Quantity A |
Quantity B |
| \(x\) |
\(y\) |
|
| (A) |
The relationship cannot be determined from the information given |
| (B) |
The two quantities are equal |
| (C) |
The quantity in Column A is greater |
| (D) |
The quantity in Column B is greater |
| 27- |
Using the information provided below, compare the quantity in column A to the quantity in Column B.
\(\frac{3}{4} \lt x \lt \frac{3}{2}\)
| Quantity A |
Quantity B |
| \(x\) |
\(\frac{4}{3}\) |
|
| (A) |
The relationship cannot be determined from the information given |
| (B) |
The quantity in Column A is greater |
| (C) |
The quantity in Column B is greater |
| (D) |
The two quantities are equal |
| 28- |
\(a\) and \(b\) are real numbers. \(a \lt b\)
| Quantity A |
Quantity B |
| \(|a \ - \ b|\) |
\(|b \ - \ a|\) |
|
| (A) |
The two quantities are equal |
| (B) |
The quantity in Column A is greater |
| (C) |
The quantity in Column B is greater |
| (D) |
The relationship cannot be determined from the information given |
| 29- |
Using the information provided below, compare the quantity in column A to the quantity in Column B.
| Quantity A |
Quantity B |
| \(\frac{x^5}{5}\) |
\((\frac{x}{5})^5\) |
|
| (A) |
The two quantities are equal |
| (B) |
The quantity in Column B is greater |
| (C) |
The quantity in Column A is greater |
| (D) |
The relationship cannot be determined from the information given |
| 30- |
Using the information provided below, compare the quantity in column A to the quantity in Column B.
| Column A |
Column B |
| \(6 \ + \ 2 \times 7 \ + \ 5 \) |
\(4 \ + \ 4 \times 7 \ - \ 3 \) |
|
| (A) |
The quantity in Column B is greater |
| (B) |
The quantity in Column A is greater |
| (C) |
The two quantities are equal |
| (D) |
The relationship cannot be determined from the information given |
| 31- |
Using the information provided below, compare the quantity in column A to the quantity in Column B.
| Column A |
Column B |
| \(\sqrt{49} \ +\ \sqrt{64} \) |
\(\sqrt{81} \) |
|
| (A) |
The two quantities are equal |
| (B) |
The quantity in Column A is greater |
| (C) |
The quantity in Column B is greater |
| (D) |
The relationship cannot be determined from the information given |
| 32- |
Using the information provided below, compare the quantity in column A to the quantity in Column B.
| Column A |
Column B |
| \(\sqrt{121\ - \ 57} \) |
\(\sqrt{121}\ -\ \sqrt{57} \) |
|
| (A) |
The relationship cannot be determined from the information given |
| (B) |
The two quantities are equal |
| (C) |
The quantity in Column A is greater |
| (D) |
The quantity in Column B is greater |
| 33- |
The average age of Joe, Michelle, and Nicole is \(24\).
| Column A |
Column B |
| The average age of Joe and Michelle |
The average age of Michelle and Nicole |
|
| (A) |
The quantity in Column A is greater |
| (B) |
The quantity in Column B is greater |
| (C) |
The two quantities are equal |
| (D) |
The relationship cannot be determined from the information given |
| 34- |
Using the information provided below, compare the quantity in column A to the quantity in Column B.
\(\ y\ = \ - \ 5 \ x \ - \ 12\)
| Column A |
Column B |
| The value of \(x\) when \(y=8\) |
\(- \ 9 \) |
|
| (A) |
The relationship cannot be determined from the information given |
| (B) |
The quantity in Column A is greater |
| (C) |
The quantity in Column B is greater |
| (D) |
The two quantities are equal |
| 35- |
A right cylinder with radius \(4\) inches has volume \(36 \ π\) cubic inches.
| Quantity A |
Quantity B |
| The height of the cylinder |
\(4\) inches |
|
| 36- |
The average of \(5, 7\), and \(x\) is \(2\).
| Quantity A |
Quantity B |
| \(x\) |
average of \(\ x\ ,\ x\ -\ 2 \ ,\ x\ + \ 6\ ,\ 4 \ x\ \) |
|
| (A) |
The relationship cannot be determined from the information given |
| (B) |
The quantity in Column A is greater |
| (C) |
The quantity in Column B is greater |
| (D) |
The two quantities are equal |
| 37- |
\(x\) is an integer greater than zero.
| Quantity A |
Quantity B |
| \(\frac{3}{x}\ + \ 2 \ x\) |
\(7\) |
|
| (A) |
The quantity in Column A is greater |
| (B) |
The quantity in Column B is greater |
| (C) |
The two quantities are equal |
| (D) |
The relationship cannot be determined from the information given |
|
ISEE Middle Level
Practice Test 3
Mathematics Achievement
- 47 questions
- Total time for this section: 40 Minutes
- Calculators are not allowed at the test.
|
| 38- |
In a bundle of \(60\) pencils, \(27\) are red and the rest are blue. About what percent of the bundle is composed of blue pencils? |
| (A) |
\(55\%\) |
| (B) |
\(50\%\) |
| (C) |
\(60\%\) |
| (D) |
\(63\%\) |
| 39- |
Solving the equation: \(10\ x\ -\ 12.5\ =- \ 42\)? |
| (A) |
\(-\ 2.95\) |
| (B) |
\(-\ 3.18\) |
| (C) |
\(-\ 2.54\) |
| (D) |
\(3.43\) |
| 40- |
What is the value of \(x\) in the following equation?
\((x \ - \ 2)^3=125\) |
| (A) |
\(5\) |
| (B) |
\(7\) |
| (C) |
\(- \ 2\) |
| (D) |
\(- \ 5\) |
| 41- |
The price of a car was \($24,000\) in \(2014, \ $18,000\) in \(2015\) and \($12,500\) in \(2016\). What is the rate of depreciation of the price of car per year? |
| (A) |
\(15\%\) |
| (B) |
\(20\%\) |
| (C) |
\(25\%\) |
| (D) |
\(30\%\) |
| 42- |
\(2 \ (\frac{1}{2} \ - \ \frac{1}{6})\ + \ 7\)? |
| (A) |
\(12\) |
| (B) |
\(10\) |
| (C) |
\(8\) |
| (D) |
\(6\) |
| 43- |
\(36\) is equal to? |
| (A) |
\(2 \ + \ (3 \ × \ 10) \ + \ (2 \ × \ 30)\) |
| (B) |
\((\frac{9}{3} \ × \ 2) \ + \ (\frac{30}{2} \ × \ 2)\) |
| (C) |
\(((\frac{3}{2} \ + \ 3) \ × \ \frac{18}{3}) \ + \ 63\) |
| (D) |
\((2 \ × \ 15) \ + \ (50 \ × \ 2) \ - \ 46\) |
| 44- |
What number is \(7\) less than \(40\%\) of \(24\)? |
| (A) |
\(2.6\) |
| (B) |
\(4.2\) |
| (C) |
\(5.8\) |
| (D) |
\(3.6\) |
| 45- |
If a box contains red and blue balls in ratio of \(3 : 5\), how many red balls are there if \(120\) blue balls are in the box? |
| (A) |
\(59\) |
| (B) |
\(64\) |
| (C) |
\(81\) |
| (D) |
\(72\) |
| 46- |
If \(\frac{2 \ x}{5}=40\), then \(\frac{2 \ x}{6} =\)? |
| (A) |
\(20\) |
| (B) |
\(24\) |
| (C) |
\(12\) |
| (D) |
\(18\) |
| 47- |
What is the difference in perimeter between a \(6\) cm by \(5\) cm rectangle and a circle with diameter of \(12\) cm? \((π=3)\) |
| (A) |
\(16\) cm |
| (B) |
\(12\) cm |
| (C) |
\(10\) cm |
| (D) |
\(24\) cm |
$20.99 $15.99
24% Off*
A Comprehensive Review and Step-By-Step Guide to Preparing for the ISEE Middle Level Math Test
|
| 48- |
What number is \(10\) more than \( 12\%\) of \(230\)? |
| (A) |
\(42\) |
| (B) |
\(39.6\) |
| (C) |
\(28.9\) |
| (D) |
\(30\) |
| 49- |
If \(170\%\) of a number is \(68\), then what is the \(80\%\) of that number? |
| (A) |
\(25\) |
| (B) |
\(28\) |
| (C) |
\(32\) |
| (D) |
\(36\) |
| 50- |
When a number is subtracted from \(18\) and the difference is divided by that number, the result is \(3\). What is the value of the number? |
| (A) |
\(3\) |
| (B) |
\(5\) |
| (C) |
\(6\) |
| (D) |
\(9\) |
| 51- |
Calculate the approximate area of the following circle.
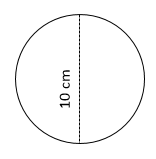 |
| (A) |
\(81.2\) |
| (B) |
\(78.5\) |
| (C) |
\(69.3\) |
| (D) |
\(72.1\) |
| 52- |
When a gas tank can hold \(24\) gallons, how many gallons does it contain when it is \(\frac{3}{4}\) full? |
| (A) |
\(24\) |
| (B) |
\(20\) |
| (C) |
\(18\) |
| (D) |
\(15\) |
| 53- |
From last year, the price of gasoline has increased from \($1.25\) per gallon to \($1.75\) per gallon. The new price is what percent of the original price? |
| (A) |
\(120\%\) |
| (B) |
\(160\%\) |
| (C) |
\(100\%\) |
| (D) |
\(140\%\) |
| 54- |
Which of the following angles can represent the three angles of an isosceles right triangle? |
| (A) |
\(45^\circ, 45^\circ, 90^\circ\) |
| (B) |
\(10^\circ, 80^\circ, 90^\circ\) |
| (C) |
\(50^\circ, 50^\circ, 80^\circ\) |
| (D) |
\(60^\circ, 60^\circ, 60^\circ\) |
| 55- |
If a gas tank can hold \(42\) gallons, how many gallons does it contain when it is \(\frac{5}{7}\) full? |
| (A) |
\(30\) |
| (B) |
\(38\) |
| (C) |
\(42\) |
| (D) |
\(47\) |
| 56- |
Which of the following is the greatest number? |
| (A) |
\(\frac{1}{2}\) |
| (B) |
\(\frac{5}{8}\) |
| (C) |
\(54\%\) |
| (D) |
\(\sqrt{0.36}\) |
| 57- |
A football team had \($21,000\) to spend on supplies. The team spent \($12,000\) on new balls. New sport shoes cost \($120\) each. Which of the following inequalities represent how many new shoes the team can purchase? |
| (A) |
\(120 \ x \ + \ 9,000 \ ≤ \ 21,000\) |
| (B) |
\(120 \ x \ + \ 12,000 \ \geq \ 21,000\) |
| (C) |
\(120 \ x \ + \ 12,000 \ ≤ \ 21,000\) |
| (D) |
\(12,000 \ x \ + \ 120\ ≤ \ 21,000\) |
| 58- |
In following rectangle which statement is true?
 |
| (A) |
Length of AB equal to length DC. |
| (B) |
AB is parallel to BC. |
| (C) |
The sum of all the angles equals \(180^\circ\). |
| (D) |
AB is perpendicular to DC. |
| 59- |
What is the missing term in the given numbers?
\(2, 3, 5, 8, 12, 17,\) ___, \(30\) |
| (A) |
\(36\) |
| (B) |
\(30\) |
| (C) |
\(25\) |
| (D) |
\(23\) |
| 60- |
The capacity of a red box is \(18\% \) greater than a blue box. If the capacity of the red box is \(59\) books, how many books can be put in the blue box? |
| (A) |
\(60\) |
| (B) |
\(68\) |
| (C) |
\(58\) |
| (D) |
\(50\) |
| 61- |
What is the perimeter of a square that has an area of \(49\) square inches? |
| (A) |
\(36\) inches |
| (B) |
\(28\) inches |
| (C) |
\(14\) inches |
| (D) |
\(30\) inches |
| 62- |
\([3 \times (–\ 18) \ +\ 6]\ – \ (– \ 8) \ + \ [2 \times 7] \div 2 = ?\) |
| (A) |
\(- \ 33\) |
| (B) |
\(- \ 36\) |
| (C) |
\(26\) |
| (D) |
\(40\) |
| 63- |
\(183\) minutes \(=\) …? |
| (A) |
\(2.85\) hours |
| (B) |
\(3.25\) hours |
| (C) |
\(3.05\) hours |
| (D) |
\(2.65\) hours |
| 64- |
Two-kilograms apple and two-kilograms orange cost \($27.3\) If one-kilogram apple costs \($3.2\) how much does one-kilogram orange cost? |
| (A) |
\($12.50\) |
| (B) |
\($15.25\) |
| (C) |
\($10.45\) |
| (D) |
\($8.45\) |
| 65- |
Jason is \(12\) miles ahead of Joe running at \(4.5\) miles per hour and Joe is running at the speed of \(6\) miles per hour. How long does it take Joe to catch Jason? |
| (A) |
\(10\) hours |
| (B) |
\(12\) hours |
| (C) |
\(6\) hours |
| (D) |
\(8\) hours |
| 66- |
In a class, there are twice as many girls as boys. If the total number of students in the class is \(69\), how many girls are in the class? |
| (A) |
\(28\) |
| (B) |
\(36\) |
| (C) |
\(23\) |
| (D) |
\(25\) |
| 67- |
Jason left a \($15.00\) tip on a lunch that cost \($50.00\), approximately what percentage was the tip? |
| (A) |
\(30\%\) |
| (B) |
\(0.3\%\) |
| (C) |
\(27\%\) |
| (D) |
\(2.7\%\) |
| 68- |
At a Zoo, the ratio of lions to tigers is \(2\) to \(5\). Which of the following could NOT be the total number of lions and tigers in the zoo? |
| (A) |
\(56\) |
| (B) |
\(72\) |
| (C) |
\(99\) |
| (D) |
\(96\) |
| 69- |
Which of the following is not a prime number? |
| (A) |
\(103\) |
| (B) |
\(101\) |
| (C) |
\(97\) |
| (D) |
\(58\) |
| 70- |
\((((- \ 15) \ +\ 24)\ ×\ 2)\ +\ (- \ 21)?\) |
| (A) |
\(- \ 1\) |
| (B) |
\(2\) |
| (C) |
\(- \ 3\) |
| (D) |
\(3\) |
| 71- |
If \(50\%\) of a class are girls, and \(36\%\) of girls play tennis, what percent of the class play tennis? |
| (A) |
\(18\%\) |
| (B) |
\(12\%\) |
| (C) |
\(24\%\) |
| (D) |
\(33\%\) |
| 72- |
A shaft rotates \(200\) times in \(5\) seconds. How many times does it rotate in\(15\) seconds? |
| (A) |
\(600\) |
| (B) |
\(400\) |
| (C) |
\(540\) |
| (D) |
\(620\) |
| 73- |
The price of a sofa is decreased by \(30\%\) to \($420\). What was its original price? |
| (A) |
\($600\) |
| (B) |
\($560\) |
| (C) |
\($500\) |
| (D) |
\($480\) |
| 74- |
The width of a rectangle is \(2 \ x\) and its length is \(5 \ x\). The perimeter of the rectangle is \(42\). What is the value of \(x\)? |
| (A) |
\(3\) |
| (B) |
\(5\) |
| (C) |
\(7\) |
| (D) |
\(9\) |
| 75- |
What is the area of the trapezoid?
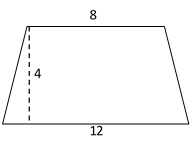 |
| (A) |
\(50\) |
| (B) |
\(40\) |
| (C) |
\(30\) |
| (D) |
\(20\) |
| 76- |
Ella bought a pair of gloves for \($12.49\). She gave the clerk \($18.00\). How much change should she get back? |
| (A) |
\($5.51\) |
| (B) |
\($6.23\) |
| (C) |
\($8.78\) |
| (D) |
\($4.98\) |
| 77- |
\(\frac{7\times12}{80}\) is closest estimate to: |
| (A) |
\(1.1\) |
| (B) |
\(6.1\) |
| (C) |
\(3.4\) |
| (D) |
\(2.9\) |
| 78- |
\(\frac{3}{4}\ +\ \frac{\frac{-\ 2}{5}} {\frac{4}{10}}=\)? |
| 79- |
What is the value of in the following equation?
\(10\ +\ 4\ (\ x\ +\ 5\ -\ 5\ x\ )=30\) |
| (A) |
\(0\) |
| (B) |
\(2\) |
| (C) |
\(8\) |
| (D) |
\(5\) |
| 80- |
A swimming pool holds \(2,000\) cubic feet of water. The swimming pool is \(25\) feet long and \(10\) feet wide. How deep is the swimming pool? |
| (A) |
\(8\) feet |
| (B) |
\(4\) feet |
| (C) |
\(9\) feet |
| (D) |
\(3\) feet |
| 81- |
If \(60\%\) of A is \(20\%\) of B, then B is what percent of A? |
| (A) |
\(300\%\) |
| (B) |
\(200\%\) |
| (C) |
\(250\%\) |
| (D) |
\(350\%\) |
| 82- |
\(12.124\div0.002= ?\) |
| (A) |
\(6,062\) |
| (B) |
\(6,132\) |
| (C) |
\(9,278\) |
| (D) |
\(7,342\) |
| 83- |
A card is drawn at random from a standard \(52\)–card deck, what is the probability that the card is of Hearts? (The deck includes \(13\) of each suit clubs, diamonds, hearts, and spades) |
| (A) |
\(\frac{ 1}{4}\) |
| (B) |
\(\frac{ 1}{3}\) |
| (C) |
\(\frac{2}{3}\) |
| (D) |
\(\frac{5}{6}\) |
| 84- |
Solve the following equation?
\(6^x=1,296\) |
| (A) |
\(4\) |
| (B) |
\(10\) |
| (C) |
\(12\) |
| (D) |
\(7\) |