|
ACCUPLACER Mathematics Practice Test 4
(Non–Calculator) 2 Sections – 40 questions
Total time for two sections: No Time Limit You may not use a calculator on this section.
|
| Arithmetic and Elementary Algebra |
| 1- |
Last Friday Jacob had \($ 45.12 \) . Over the weekend he received some money for cleaning the attic. He now has \($ 62\) . How much money did he receive? |
| (A) |
\( $ 16.68\) |
| (B) |
\( $ 16.78\) |
| (C) |
\( $ 16.88\) |
| (D) |
\( $ 16.98\) |
| 2- |
\( x^2 \ - \ 8 \ x \ + \ 15 \ = \) ? |
| (A) |
\((x \ – \ 3) \ (x \ - \ 5)\) |
| (B) |
\((x \ + \ 3) \ (x \ - \ 5)\) |
| (C) |
\((x \ + \ 3) \ (x \ + \ 5)\) |
| (D) |
\((x \ - \ 3) \ (x \ + \ 5)\) |
| 3- |
What is \(6254.74164\) rounded to the nearest tenth? |
| (A) |
\( 6254.7\) |
| (B) |
\( 6254.8\) |
| (C) |
\( 6254.9\) |
| (D) |
\( 6254.0\) |
| 4- |
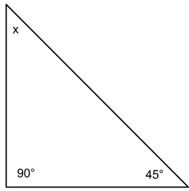
In the following diagram, what is the value of \( x\) in the following triangle?
 |
| (A) |
\(40^\circ\) |
| (B) |
\(46^\circ\) |
| (C) |
\(60^\circ\) |
| (D) |
\(45^\circ\) |
| 5- |
\(45\) is what percent of \(120\) ? |
| (A) |
\( 37\%\) |
| (B) |
\( 37.5\%\) |
| (C) |
\( 38.5\%\) |
| (D) |
\( 38\%\) |
| 6- |
Which of the following equations has a graph that is a straight line? |
| (A) |
\(3 \ y \ + \ 6 = 4 \ x\) |
| (B) |
\( y \ = \ 3 \ x^2 \ + \ 9 \) |
| (C) |
\(3 \ y^2 \ + \ 6 = x\) |
| (D) |
\(3 \ y \ + \ 6 = x^2\) |
| 7- |
Find all values for which \(2 \ x^2 \ - \ 5 \ x \ - \ 3 \ = \ 0\) |
| (A) |
\(- \ 12 , \frac{1}{2}\) |
| (B) |
\(\frac{1}{2} , 12\) |
| (C) |
\(- \ \frac{1}{2} , 3\) |
| (D) |
\(- \ \frac{3}{2} , 12\) |
| 8- |
What is the distance between the points \( (2, 4)\) and \( (- \ 4, - \ 4) \) ? |
| (A) |
\(100\) |
| (B) |
\(10\) |
| (C) |
\(5\) |
| (D) |
\(7\) |
| 9- |
Simplify \( \frac{\frac{4}{3} \ - \ \frac{2 \ x \ - \ 3}{9}}{\frac{x^2}{3} \ - \ \frac{7}{3}} \) |
| (A) |
\( \frac{- \ 2 \ x \ - \ 15}{3 \ x^2 \ - \ 21} \) |
| (B) |
\( \frac{- \ 2 \ x \ - \ 15}{3 \ x^2 \ +\ 21} \) |
| (C) |
\( \frac{- \ 2 \ x \ + \ 15}{3 \ x^2 \ + \ 21} \) |
| (D) |
\( \frac{- \ 2 \ x \ + \ 15}{3 \ x^2 \ - \ 21} \) |
| 10- |
A man owed \($ 3254 \) on his car. After making \(42\) payment of \($ 65 \) each, how much did he have left to pay? |
| (A) |
\($ 234\) |
| (B) |
\($ 236\) |
| (C) |
\($ 524\) |
| (D) |
\($ 253\) |
| 11- |
Write the \( \frac{7}{120} \) as a decimal. |
| (A) |
\(0.059\) |
| (B) |
\(0.058\) |
| (C) |
\(0.60\) |
| (D) |
\(0.62\) |
| 12- |
\( \sqrt{75} \) is between which two whole numbers? |
| (A) |
\(7\) and \(8\) |
| (B) |
\(8\) and \(9\) |
| (C) |
\(6\) and \(7\) |
| (D) |
\(5\) and \(6\) |
| 13- |
Which of the following is one solution of this equation?
\(3 \ x^2 \ + \ 10 \ x \ - \ 2 \ = \ 0\) |
| (A) |
\( \frac{- \ 5 \ ± \ \sqrt{31}}{3} \) |
| (B) |
\( \frac{- \ 5 \ - \ \sqrt{31}}{3} , 0.12\) |
| (C) |
\( \frac{- \ 5 \ + \ \sqrt{31}}{3} , 0.358\) |
| (D) |
\( \frac{- \ 5 \ + \ \sqrt{31}}{3} , 0.438\) |
| 14- |
\( (x \ + \ 7 ) \ (x^{2} \ - \ 4 \ x \ + \ 3) = \) ? |
| (A) |
\( x^3 \ - \ 3 \ x^2 \ – \ 25 \ x \ + \ 21\) |
| (B) |
\( x^3 \ - \ 3 \ x^2 \ + \ 25 \ x \ + \ 21\) |
| (C) |
\( x^3 \ - \ 3 \ x^2 \ + \ 25 \ x \ - \ 21\) |
| (D) |
\( x^3 \ + \ 3 \ x^2 \ – \ 25 \ x \ + \ 21\) |
| 15- |
\( (x^{5})^{\frac{2}{7}} \) |
| (A) |
\( x^{ \frac{11}{7}}\) |
| (B) |
\( x^{ \frac{10}{7}}\) |
| (C) |
\( x^{ \frac{9}{7}}\) |
| (D) |
\( x^{ \frac{8}{7}}\) |
| 16- |
How many \( 6 \ × \ 6\) squares can fit inside a rectangle with a height of \(42\) and width of \(18\)? |
| (A) |
\(21\) |
| (B) |
\(16\) |
| (C) |
\(24\) |
| (D) |
\(36\) |
| 17- |
If a vehicle is driven \(42\) miles on Monday, \(47\) miles on Tuesday, and \(31\) miles on Wednesday, what is the average number of miles driven each day? |
| (A) |
\(42\) miles |
| (B) |
\(45\) miles |
| (C) |
\(46\) miles |
| (D) |
\(40\) miles |
| 18- |
Alex’s average (arithmetic mean) on two mathematics tests is \(10\) . What should Liam’s score be on the next test to have an overall of \(12\) for all the tests? |
| (A) |
\(12\) |
| (B) |
\(18\) |
| (C) |
\(16\) |
| (D) |
\(10\) |
| 19- |
If \( 6\ - \ 3 \ x \ ≤ \ 18 \) , what is the value of \( x \geq \) ? |
| (A) |
\(4\) |
| (B) |
\(3\) |
| (C) |
\(-4\) |
| (D) |
\(-3\) |
| 20- |
\( 9^{5 } \ × \ 9^{ - \ 8} \ = \)? |
| (A) |
\(9^{ 3}\) |
| (B) |
\(9^{ - \ 3}\) |
| (C) |
\(9^{ 14}\) |
| (D) |
\(9^{ 10}\) |
$24.99 $13.99
44% Off*
The Ultimate Step by Step Guide to Preparing for the Accuplacer Math Test
|
| College–Level Mathematics |
| 21- |
cos \(2 \ \theta = \) ? |
| (A) |
\( 1\ + \ 2 \ sin^2\ \theta\) |
| (B) |
\( 1\ - \ 2 \ sin^2\ \theta\) |
| (C) |
\( - \ 2 \ sin^2\ \theta\) |
| (D) |
\( 2 \ sin^2\ \theta\) |
| 22- |
If \( \theta \) is an acute angle and sin \( \theta =\frac{4}{5} \) , cos \( \theta = \) ? |
| (A) |
\(\frac{4}{5}\) |
| (B) |
\(\frac{3}{5}\) |
| (C) |
\(\frac{2}{5}\) |
| (D) |
\(\frac{1}{5}\) |
| 23- |
If the center of a circle is at the point \( (4, - \ 1) \) and its circumference equals to \(4 \ π\) , what is the standard form equation of the circle? |
| (A) |
\((x \ +\ 4)^2 \ + \ (y \ + \ 1)^2 = 2 \) |
| (B) |
\((x \ - \ 4)^2 \ + \ (y \ + \ 1)^2 \ = \ 4 \) |
| (C) |
\((x \ - \ 4)^2 \ + \ (y \ + \ 1)^2 \ = \ 2 \) |
| (D) |
\((x \ - \ 4)^2 \ + \ (y \ - \ 1)^2 \ = \ 4 \) |
| 24- |
What is the solution of the following system of equations?
\( \begin{cases} 4 \ x \ + \ y = 8 \\ - \ 8 \ x \ - \ 4 \ y = 16\end{cases} \) |
| (A) |
\((6, 16)\) |
| (B) |
\((- \ 6, 16)\) |
| (C) |
\((6, - \ 16)\) |
| (D) |
\((6, 16)\) |
| 25- |
What is the center and radius of a circle with the following equation?
\( (x \ – \ 6)^2 \ + \ (y \ + \ 4)^2 \ = \ 5 \) |
| (A) |
\((6, 4), \ \sqrt{5} \) |
| (B) |
\((6 , - \ 4), \ \sqrt{5} \) |
| (C) |
\((- \ 6 , - \ 4), \ \sqrt{5} \) |
| (D) |
\((- \ 6 , 4), \ \sqrt{5} \) |
| 26- |
If sin A \(=\ \frac{2}{5} \) in a right triangle and the angle A is an acute angle, then what is cos A ? |
| (A) |
\(\frac{\sqrt{22}}{5}\) |
| (B) |
\(\frac{\sqrt{20}}{5}\) |
| (C) |
\(\frac{\sqrt{21}}{5}\) |
| (D) |
\(\frac{\sqrt{3}}{5}\) |
| 27- |
If \( \log_{3}{x \ = \ 6}\) , then \( x \ = \) ? |
| (A) |
\(729\) |
| (B) |
\(243\) |
| (C) |
\(719\) |
| (D) |
\(216\) |
| 28- |
Simplify: \( \frac{2 \sqrt{12}}{9 \sqrt{48}} \) |
| (A) |
\(\frac{2}{9}\) |
| (B) |
\(\frac{4}{9}\) |
| (C) |
\(\frac{1}{9}\) |
| (D) |
\(\frac{5}{9}\) |
| 29- |
What’s the reciprocal of \( \frac{25}{x^3} \) ? |
| (A) |
\(\frac{x^3}{25 }\) |
| (B) |
\(\frac{25}{x^3 }\) |
| (C) |
\(\frac{5}{x }\) |
| (D) |
\(\frac{5}{x ^3 }\) |
| 30- |
If \( \log_{4}{x \ = \ 3}\) , then \(x \ =\) ? |
| (A) |
\(81\) |
| (B) |
\(16\) |
| (C) |
\(64\) |
| (D) |
\(36\) |
| 31- |
What is sin \(60^\circ \)? |
| (A) |
\(\frac{\sqrt{3}}{2}\) |
| (B) |
\(\sqrt{3}\) |
| (C) |
\(- \ \sqrt{3}\) |
| (D) |
\(- \ \frac{\sqrt{3}}{2}\) |
| 32- |
Find the inverse function for ln \( (4 \ x \ - \ 3) \) |
| (A) |
\(\frac{1}{4} (e^{\ x} \ - \ 3)\) |
| (B) |
\(\frac{1}{2} (e^{\ x} \ + \ 3)\) |
| (C) |
\(\frac{1}{4} (e^{\ x} \ + \ 3)\) |
| (D) |
\(\frac{1}{2} (e^{\ x} \ - \ 3)\) |
| 33- |
Solve.
\( | \ 15 \ – \ (18 \ ÷ \ | \ 3 \ + \ 6 \ |)| = \) ? |
| (A) |
\(- \ 13\) |
| (B) |
\(- \ 12\) |
| (C) |
\(12\) |
| (D) |
\(13\) |
| 34- |
Simplify \(( – \ 7 \ + \ 2 \ i) \ (9 \ + \ 4 \ i)\) . |
| (A) |
\( - \ 10 \ i \ - \ 71\) |
| (B) |
\( - \ 10 \ i \ + \ 71\) |
| (C) |
\( 10 \ i \ + \ 71\) |
| (D) |
\( 10 \ i \ - \ 71\) |
| 35- |
If \( f(x) \ = \ x \ – \frac{4}{5}\) and \(f ^{ \ – \ 1} \) is the inverse of \( f(x) \) , what is the value of \( f^{ \ - \ 1}(2) \) |
| (A) |
\(\frac{7}{5} \) |
| (B) |
\(\frac{16}{5} \) |
| (C) |
\(\frac{6}{5} \) |
| (D) |
\(\frac{14}{5} \) |
| 36- |
Find tan \( \frac{4 \ π}{3} \) |
| (A) |
\( - \ \sqrt{3} \) |
| (B) |
\( \sqrt{3} \) |
| (C) |
\(2 \ \sqrt{3} \) |
| (D) |
\( - \ 2 \ \sqrt{3} \) |
| |
| 37- |
Solve the equation: \( \log_{5}{(x \ - \ 4)} \ – \ \log_{5}{(x \ + \ 3)} \ = \ 1 \) |
| (A) |
\(\frac{9}{4}\) |
| (B) |
\(\frac{18}{4}\) |
| (C) |
\(\frac{14}{4}\) |
| (D) |
\(-\frac{19}{4}\) |
| 38- |
If \( f(x) \ = 2 \ x \ + \ 6 \) and \( g(x) \ = x^2 \ + \ 3 \ x\) , then find \( (\frac{f}{g}) (x) \) |
| (A) |
\(\frac{2 \ x \ - \ 6}{x^2 \ +\ 3 \ x} \) |
| (B) |
\(\frac{2 \ x \ + \ 6}{x^2 \ +\ 3 \ x} \) |
| (C) |
\(\frac{2 \ x \ + \ 6}{x^2 \ - \ 3 \ x} \) |
| (D) |
\(\frac{2 \ x \ - \ 6}{x^2 \ - \ 3 \ x} \) |
| 39- |
The slop of a line with the equation \( y \ = \ 6 \ x \ + \ 12 \) is … |
| (A) |
\(4\) |
| (B) |
\(\frac{5}{3}\) |
| (C) |
\(\frac{5}{6}\) |
| (D) |
\(6\) |
| 40- |
Solve \( e^{(7 \ x \ + \ 1 )} \ = \ 8 \) |
| (A) |
\(\frac{ln(8) \ +\ 1}{7}\) |
| (B) |
\(\frac{ln(8) \ +\ 1}{5}\) |
| (C) |
\(\frac{ln(8) \ -\ 1}{5}\) |
| (D) |
\(\frac{ln(8) \ -\ 1}{7}\) |