
How to Find the Area of a triangle
Read,3 minutes
A triangle is a polygon having \(3\) edges as well as \(3\) vertices. It’s a standard shape in geometry.
What’s the Area of a Triangle?
The area of a triangle is described as the whole area enclosed by the \(3\) sides of any particular triangle. Essentially, it’s equal to half of the \(base \times height\), i.e. \(A \ = \ \frac{1}{2} \times b \times h\).
So, to figure out the area of a tri-sided polygon, you must know its base (\(b\)) and height (\(h\)). This applies to all triangles, no matter if it’s scalene, equilateral, or isosceles. To be observed, the triangle’s base and height are perpendicular to each other. The unit of the area gets measured in square units (\(m^2, \ cm^2\)).
.png)
What are the Angles of a Triangle?
The angle of a triangle is the space created in-between \(2\) side lengths of a triangle. A triangle has interior angles and exterior angles. Interior angles are \(3\) angles existing inside a triangle. Exterior angles are created whenever a triangle’s sides get extended to infinity.
The figure underneath shows a triangle’s angle. The interior angles are \(a, \ b\) and \(c\), and the exterior angles are \(d, \ e\) and \(f\).
.png)
To calculate a triangle’s angles, you must recall the following \(3\) properties regarding triangles:
- Triangle angle sum theorem: This says the sum of all the \(3\) interior angles of a triangle are equal to \(180\) degrees. \(a \ + \ b \ + \ c \ = \ 180°\)
- Triangle exterior angle theorem: This says the exterior angle is equal to the sum of \(2\) opposite and non-adjacent interior angles. \(f \ = \ b \ + \ a\)
Free printable Worksheets
Exercises for Angle and Area of Triangles
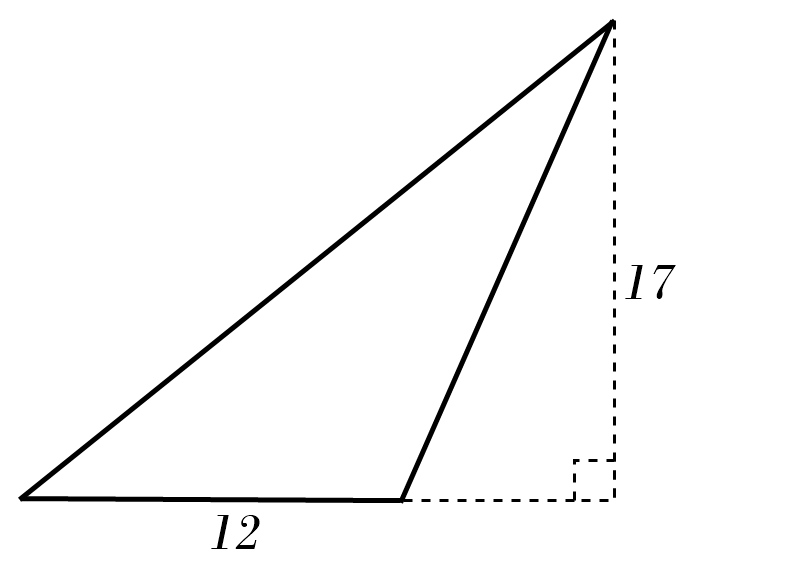
1) 
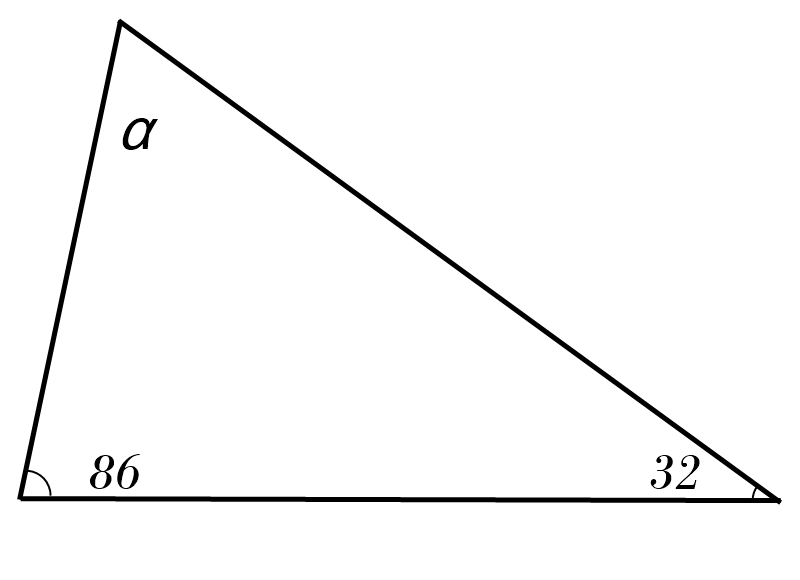
2) 
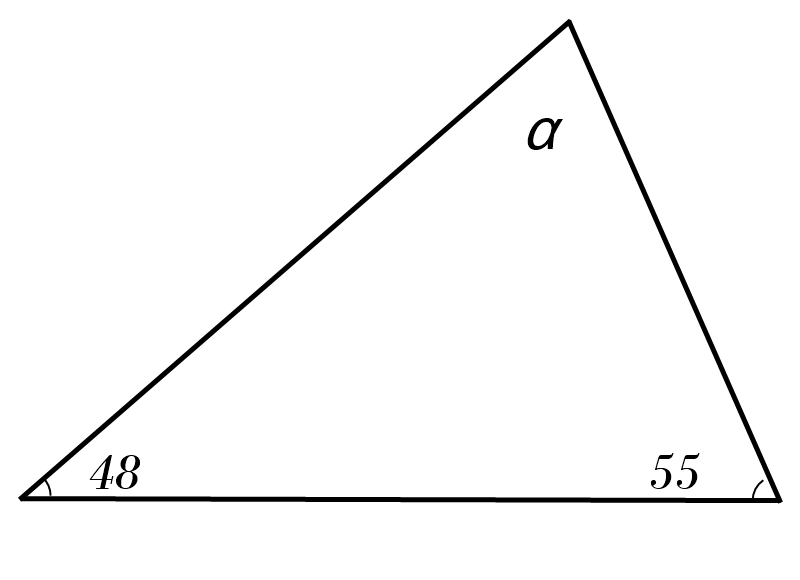
3) 
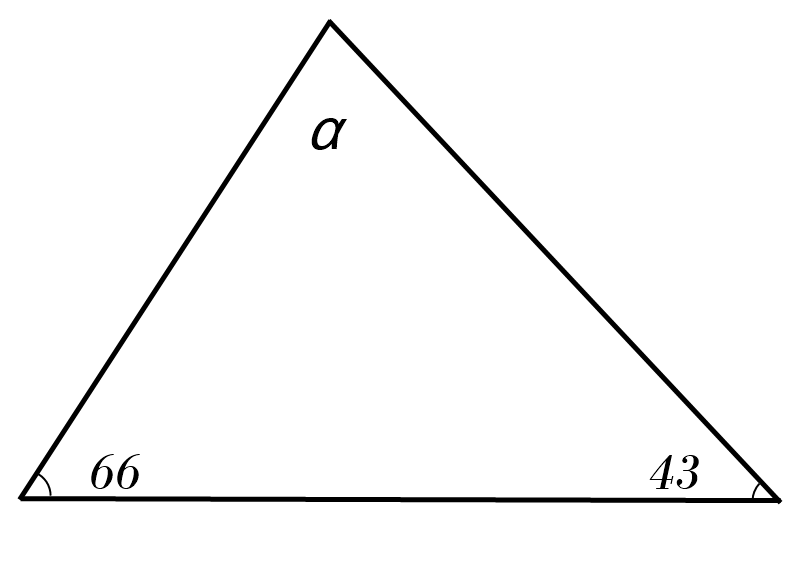
4) 
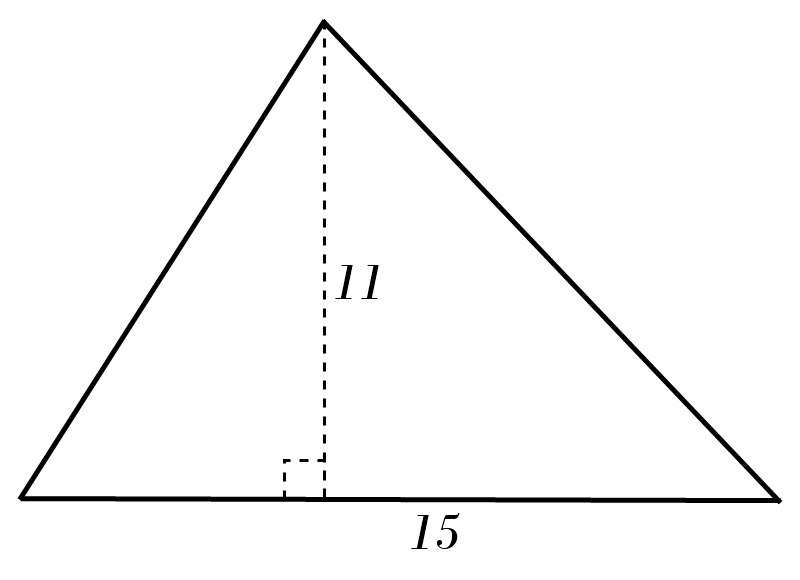
5) 
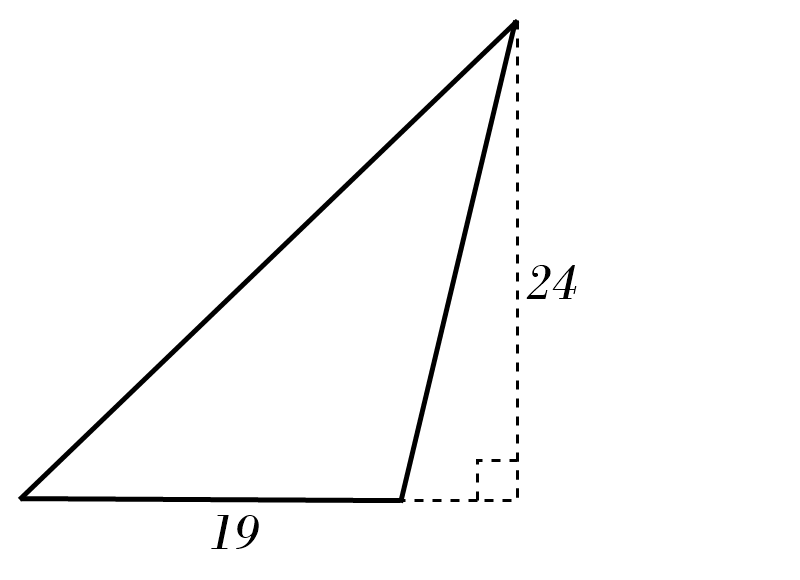
6) 
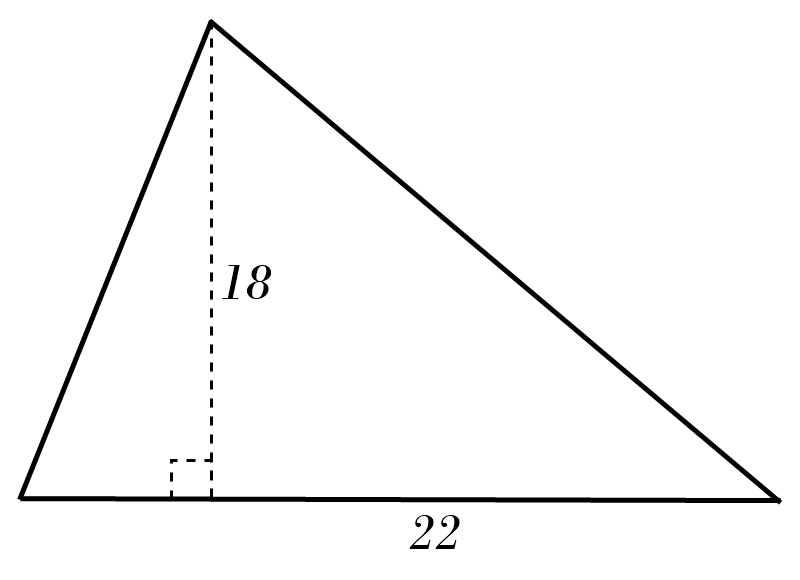
7) 
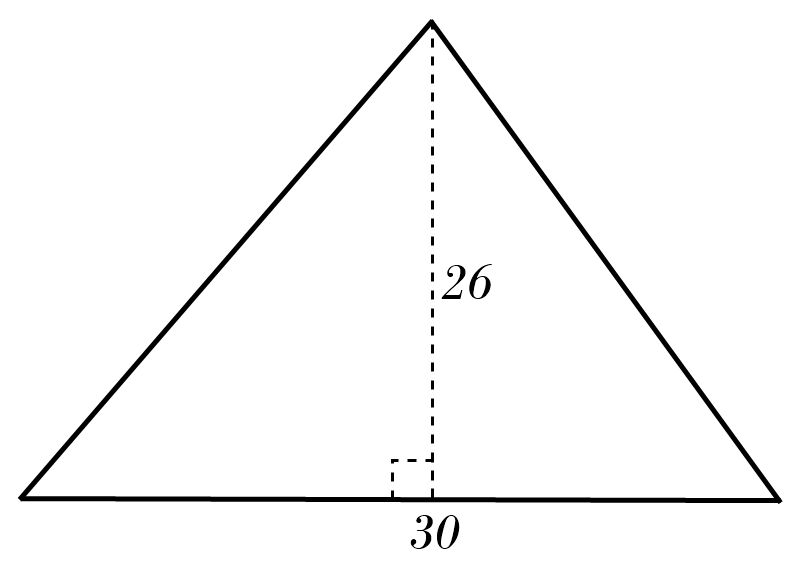
8) 
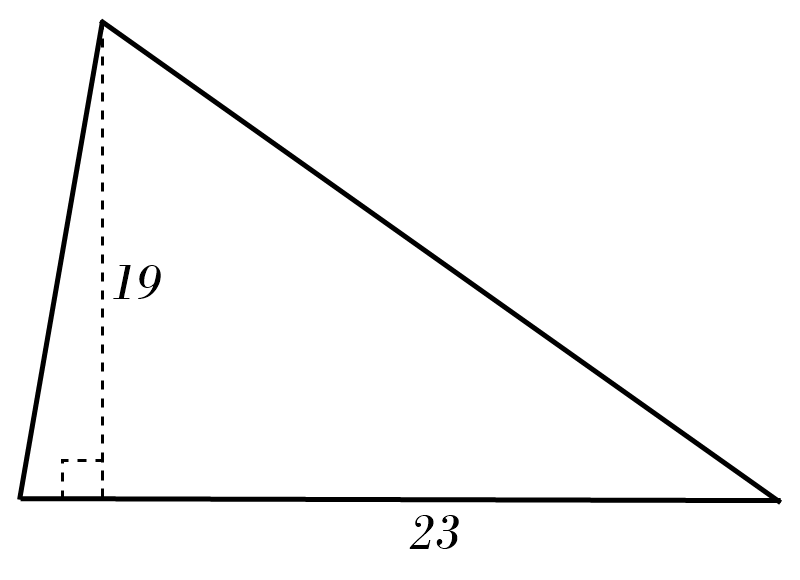
9) 
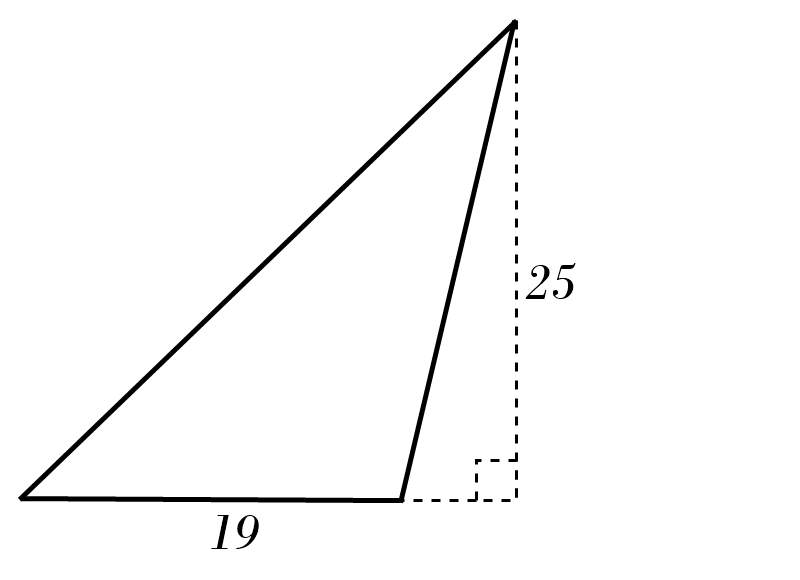
10) 
Angle and Area of Triangles Practice Quiz