
How to Find the Area and Circumference of Circles
Read,5 minutes
Radius of a Circle
The distance going from the center to the outer line of a circle is known as the radius. It’s the top vital quantity of the circle depending on what formulas used for the area and circumference of the circle are taken. The diameter of a circle is twice its radius. A diameter slices a circle into \(2\) equal parts, and that is known as a semi-circle.
Circle’s Circumference
The Circumference of a circle or the perimeter of a circle is the measurement of its boundary. Where the circle’s describes the region it occupied. If a circle is opened and you make it into a straight line, its length is its circumference. It’s normally measured in units, like centimeters or unit millimeters.
.png)
Formula for the Circumference of a Circle
Circumference (or) perimeter of a circle \(= \ 2πR\)
when \(R\) is the radius of the circle, \(π\) is the mathematical constant with an approximate (up to two decimal points) value of \(3.14\)
For instance: If the circle’s radius is \(3\) centimeters, calculate the circumference.
Provided: Radius \(= \ 3\) centimeters, Circumference \(= \ 2πr \ = \ 2 \times 3.14 \times 3 \ = \ 18.84\) centimeters
Formula for the Area of a Circle
The area of any circle is the area encircled by the circle itself or the area enveloped by it. To find the circle’s area use this formula: \(A \ = \ πr^2\)
When \(r\) is the circle’s radius of the circle, this formula can be applied to every circle with different radii.
Circumference to Diameter
A circle’s diameter is twice the radius. The proportion in-between the circle’s circumference and its diameter equals the value of Pi (\(π\)). So, this means this proportion is the definition of the constant \(π\). (i.e) \(C \ = \ 2πr \ ⇒ \ C \ = \ πd\) (As, \(d \ = \ 2r\))
If one divides both sides by the circle’s diameter, you end up with a value that’s approximately close to the value of \(π\). So, \(\frac{C}{d} \ = \ π\).
Free printable Worksheets
Exercises for Area and Circumference of Circles
1)
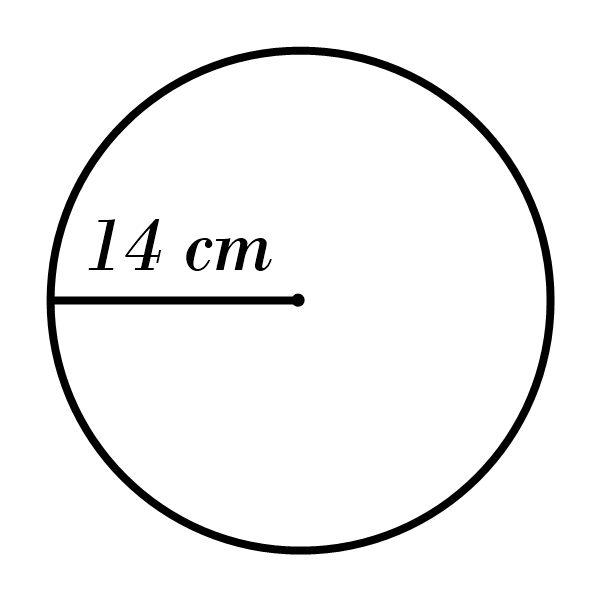
2)
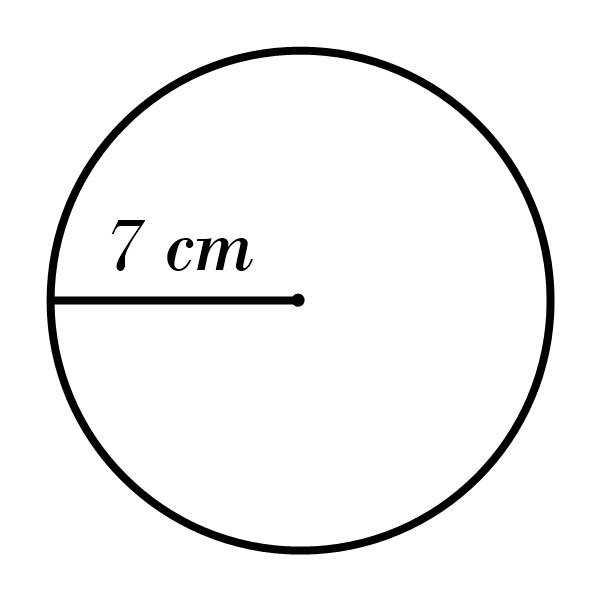
3)
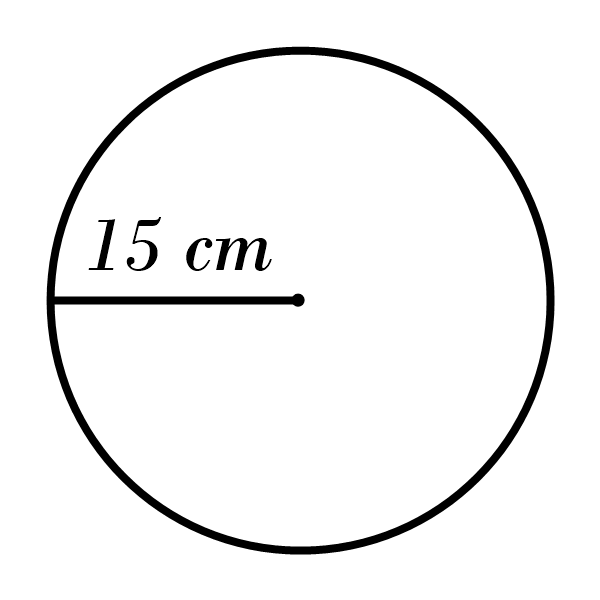
4)
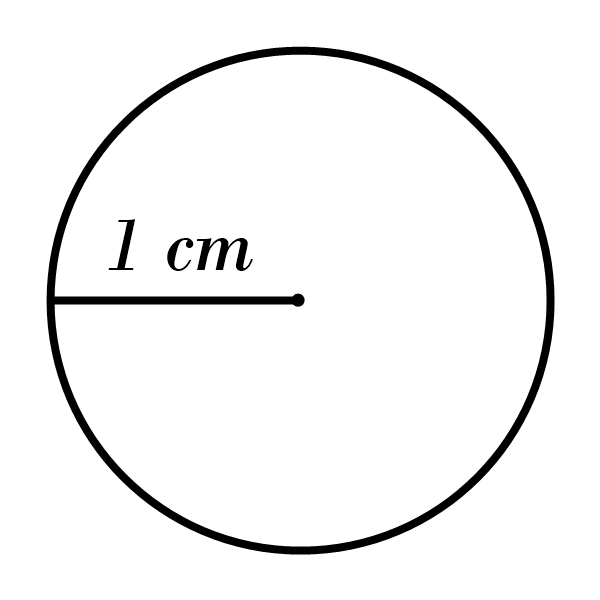
5)
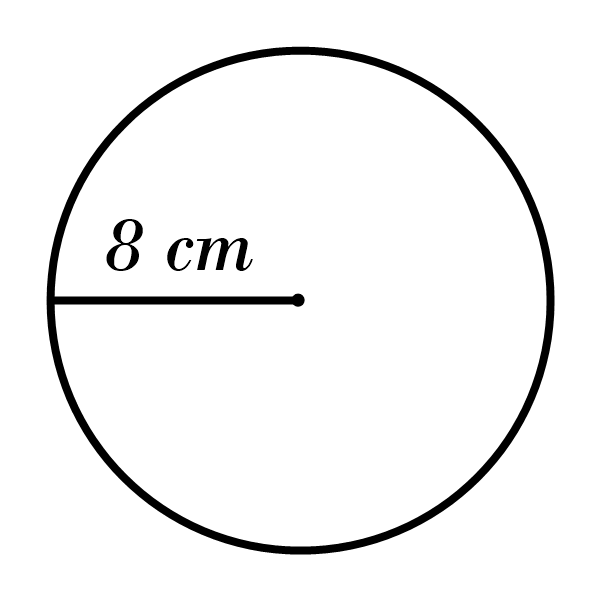
6)
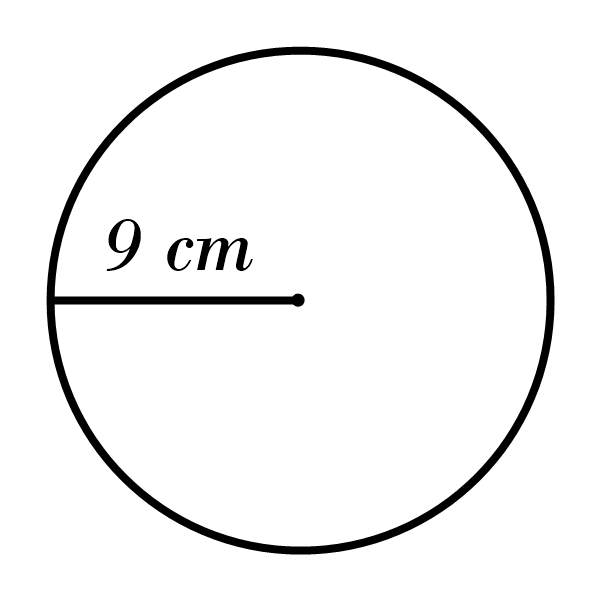
7)
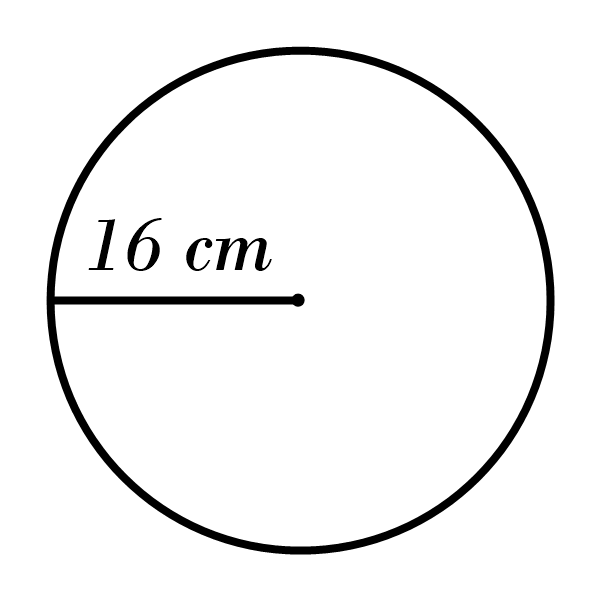
8)
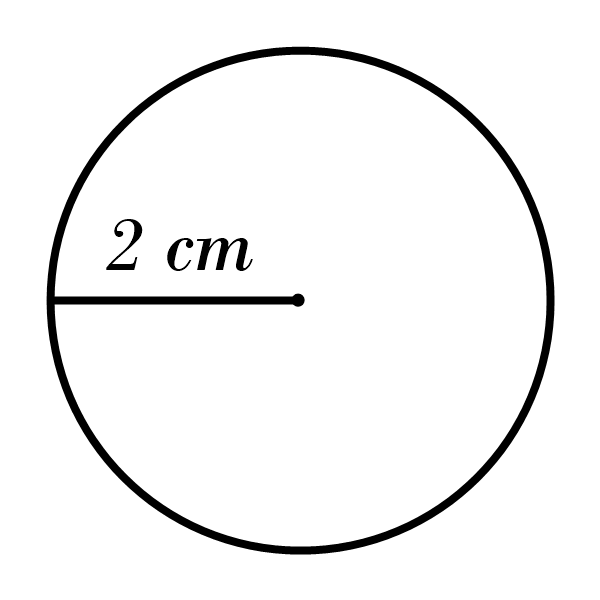
9)
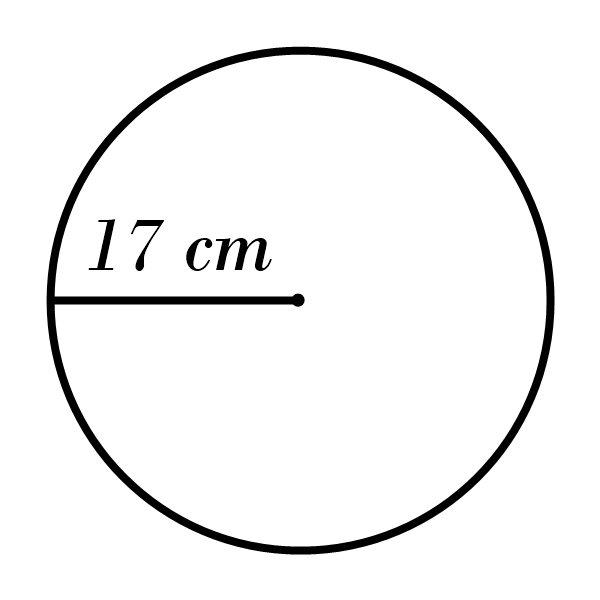
10)
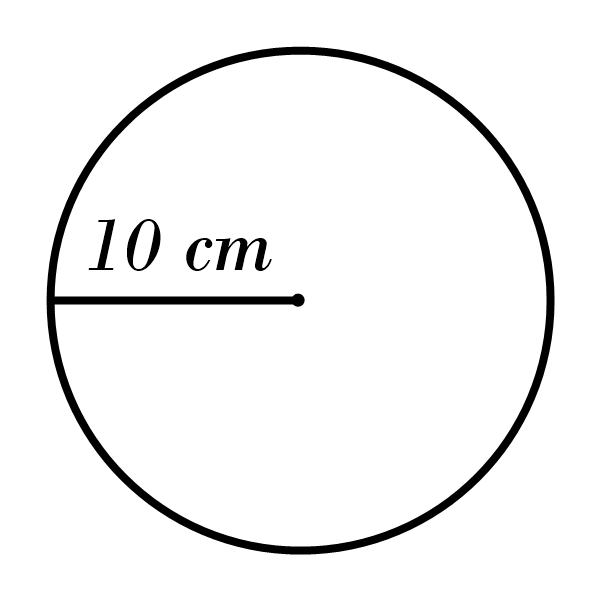
1) Area: \(615.44 \) cm\(^2\), Circumference: \(87.92 \) cm 
2) Area: \(153.86 \) cm\(^2\), Circumference: \(43.96 \) cm 
3) Area: \(706.5 \) cm\(^2\), Circumference: \(94.2 \) cm 
4) Area: \(3.14 \) cm\(^2\), Circumference: \(6.28 \) cm 
5) Area: \(200.96 \) cm\(^2\), Circumference: \(50.24 \) cm 
6) Area: \(254.34 \) cm\(^2\), Circumference: \(56.52 \) cm 
7) Area: \(803.84 \) cm\(^2\), Circumference: \(100.48 \) cm 
8) Area: \(12.56 \) cm\(^2\), Circumference: \(12.56 \) cm 
9) Area: \(907.46 \) cm\(^2\), Circumference: \(106.76 \) cm 
10) Area: \(314 \) cm\(^2\), Circumference: \(62.8 \) cm 
Area and Circumference of Circles Practice Quiz