
What is The Pythagorean Theorem
Read,3 minutes
Pythagoras theorem, which sometimes is called the Pythagorean theorem spells out the relationship between the \(3\) sides of a right-angled triangle. Pythagoras theorem says if a triangle is right-angled (\(90\) degrees), the square of the hypotenuse is equal to the sum of the squares of the other \(2\) sides.
Look at the subsequent triangle \(ABC\), where:
\((BC)^2 \ = \ (AB)^2 \ + \ (AC)^2\)
With this, \(AB\) is the base, \(AC\) is the altitude (height), and \(BC\) is the hypotenuse. It must be stated that the hypotenuse is the longest side of a right-angled triangle.
.png)
\((Hypotenuse)^2 \ = \ (Base)^2 \ + \ (height)^2\)
Another method of understanding way to understand the Pythagorean theorem formula is by utilizing the subsequent figure showing the area of the square formed by the longest side of the right triangle (the hypotenuse) is equal to the sum of the area of the squares formed by the other \(2\) sides of the right triangle.
.png)
\(R^2 \ = \ P^2 \ + \ Q^2\)
With a right-angled triangle, the Pythagoras Theorem Formula is written as: \(c^2 \ = \ a^2 \ + \ b^2\)
Where:
- \(c\) = hypotenuse of the right triangle
- \(a\) and \(b\) are the other \(2\) legs.
Free printable Worksheets
Exercises for The Pythagorean Theorem
1) \( x = \)
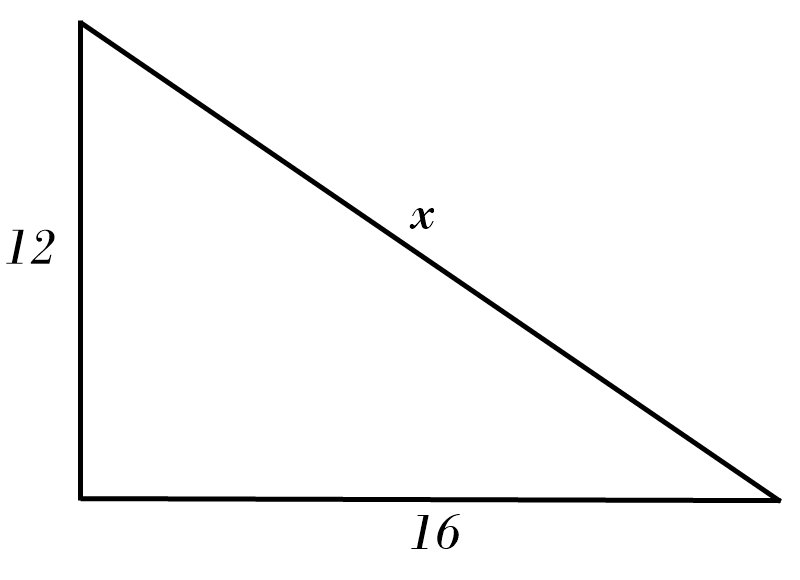
2) \( x = \)
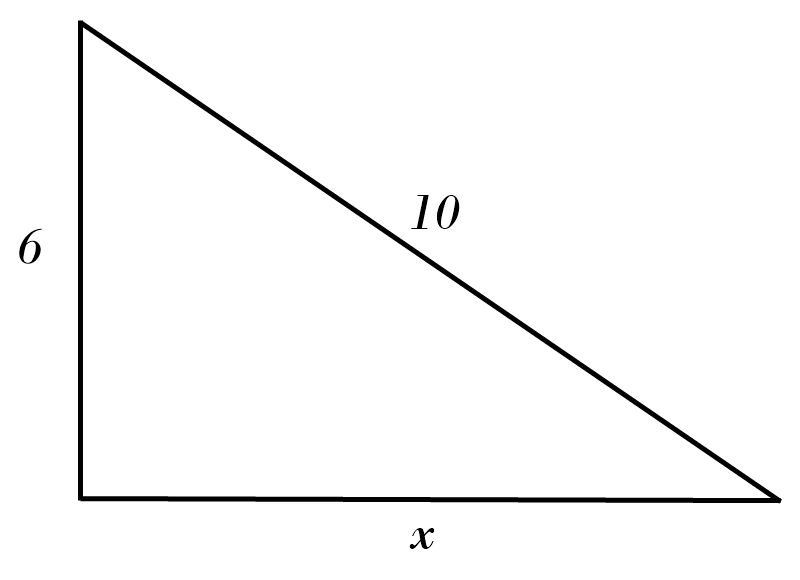
3) \( x = \)
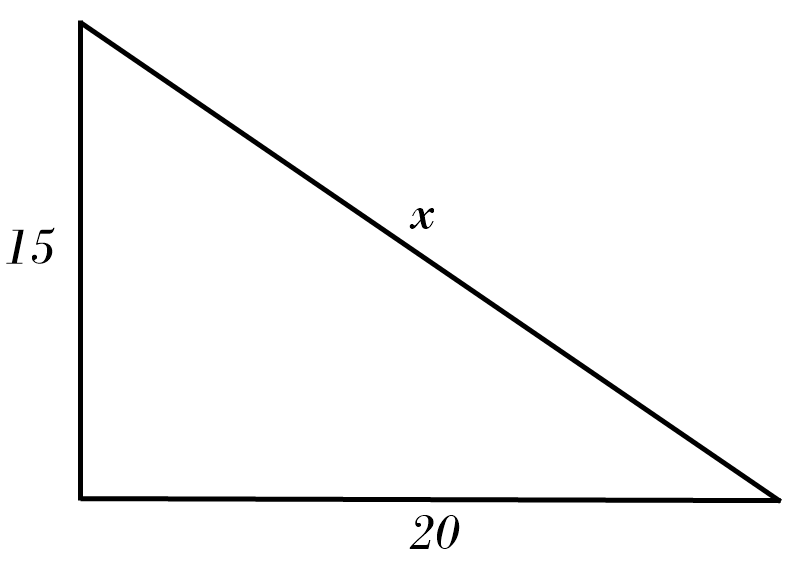
4) \( x = \)
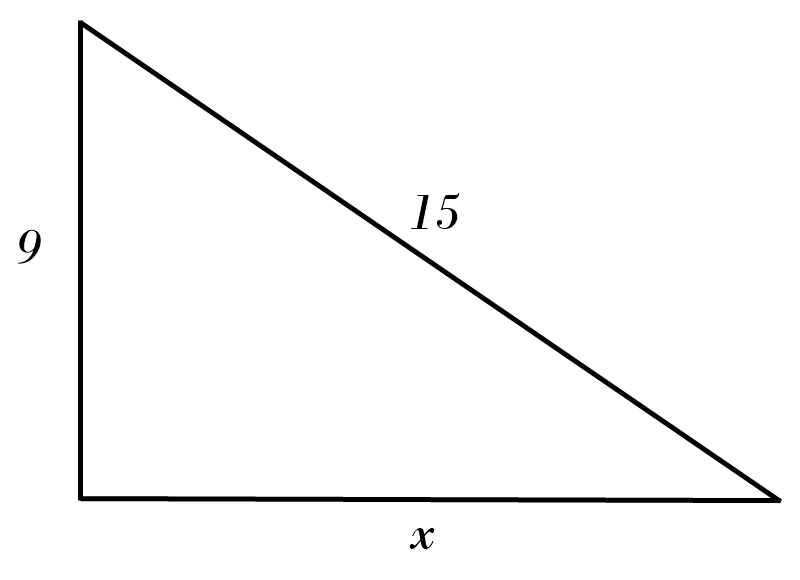
5) \( x = \)
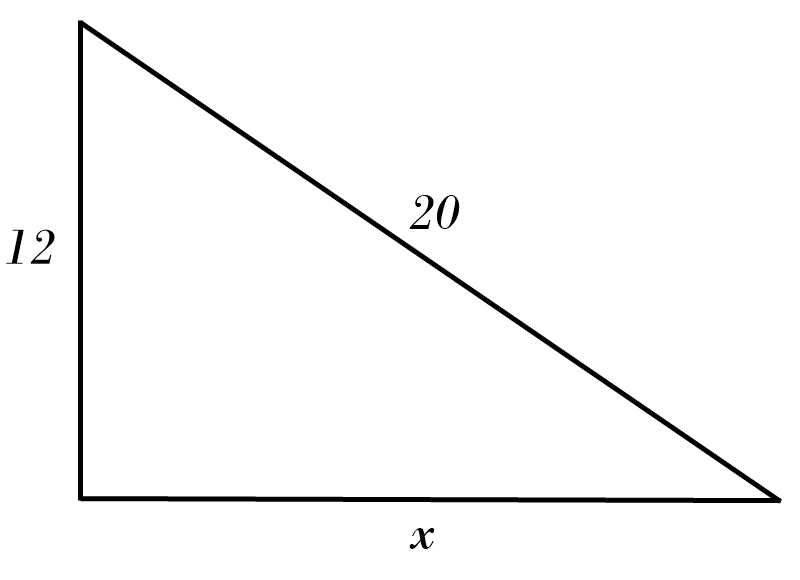
6) \( x = \)
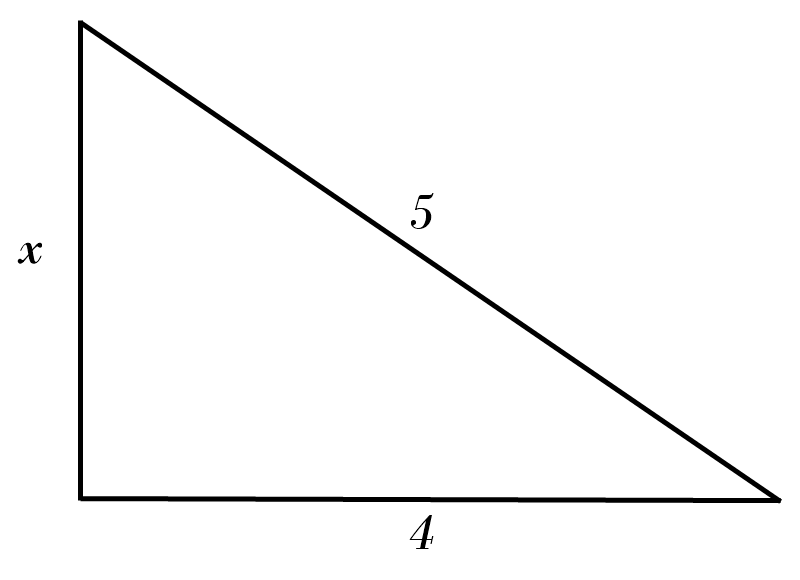
7) \( x = \)
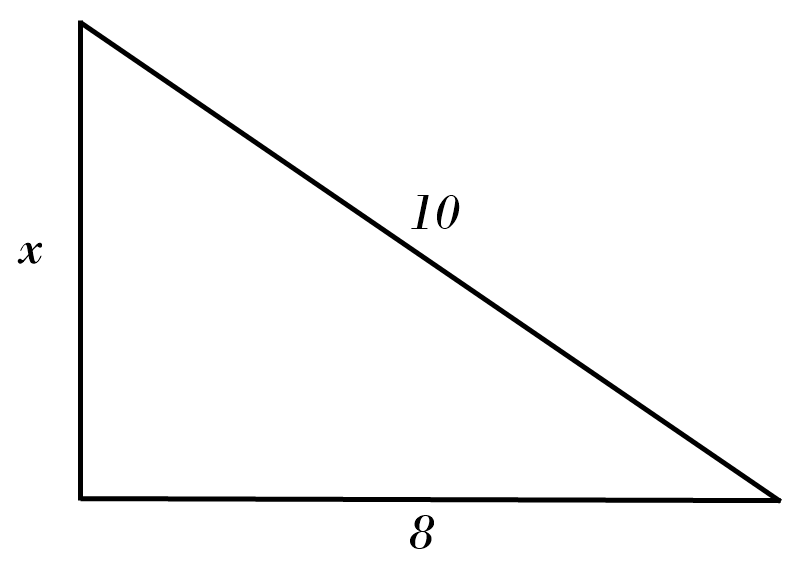
8) \( x = \)
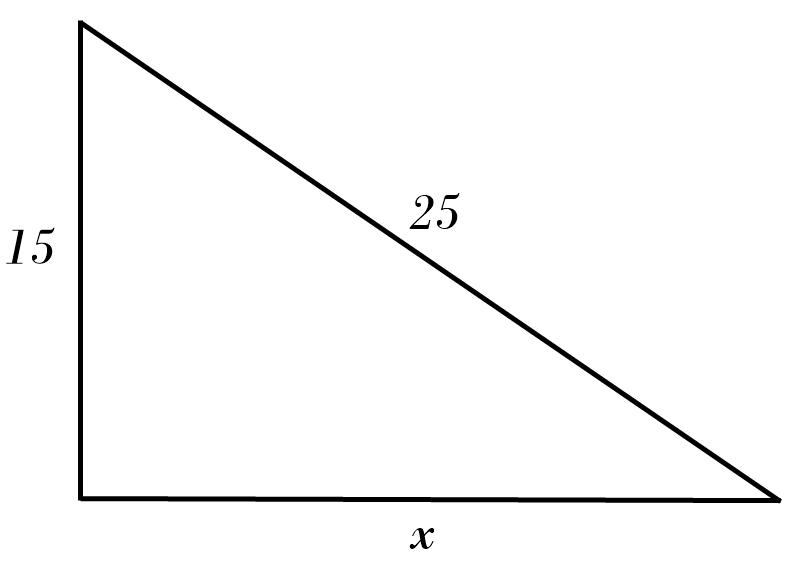
9) \( x = \)
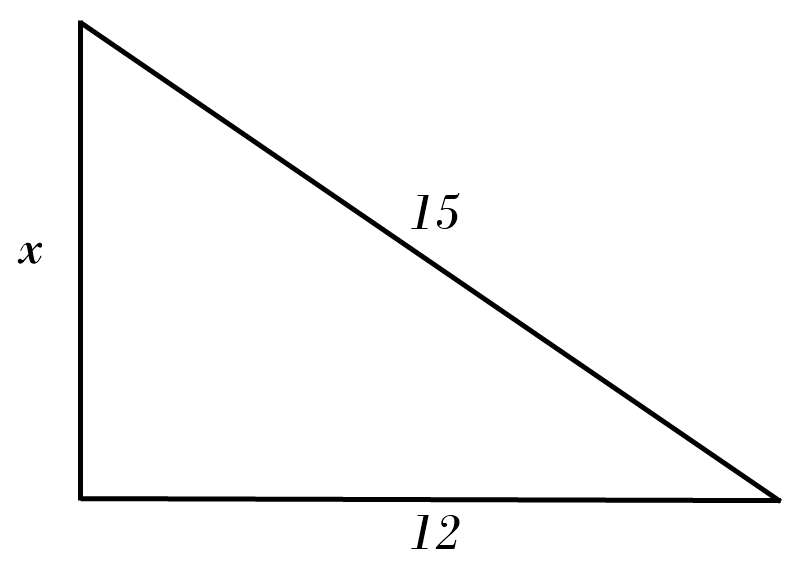
10) \( x = \)
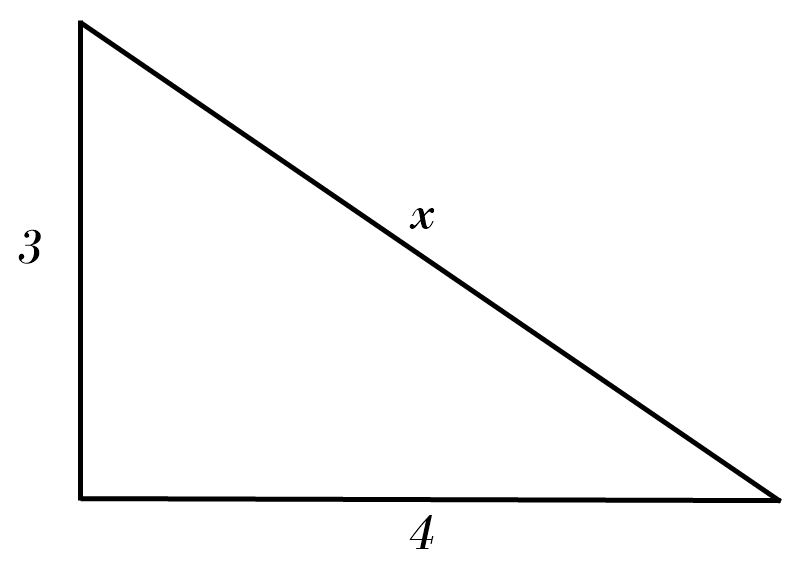
1) \( x = \color{red}{12^2 \ + \ 16^2 = x^2 }\)\( \ \Rightarrow \ x = \color{red}{\sqrt{400} = 20} \)

2) \( x = \color{red}{10^2 \ - \ 6^2 = x^2 }\)\( \ \Rightarrow \ x = \color{red}{\sqrt{64} = 8} \)

3) \( x = \color{red}{15^2 \ + \ 20^2 = x^2 }\)\( \ \Rightarrow \ x = \color{red}{\sqrt{625} = 25} \)

4) \( x = \color{red}{15^2 \ - \ 9^2 = x^2 }\)\( \ \Rightarrow \ x = \color{red}{\sqrt{144} = 12} \)

5) \( x = \color{red}{20^2 \ - \ 12^2 = x^2 }\)\( \ \Rightarrow \ x = \color{red}{\sqrt{256} = 16} \)

6) \( x = \color{red}{5^2 \ - \ 4^2 = x^2 }\)\( \ \Rightarrow \ x = \color{red}{\sqrt{9} = 3} \)

7) \( x = \color{red}{10^2 \ - \ 8^2 = x^2 }\)\( \ \Rightarrow \ x = \color{red}{\sqrt{36} = 6} \)

8) \( x = \color{red}{25^2 \ - \ 15^2 = x^2 }\)\( \ \Rightarrow \ x = \color{red}{\sqrt{400} = 20} \)
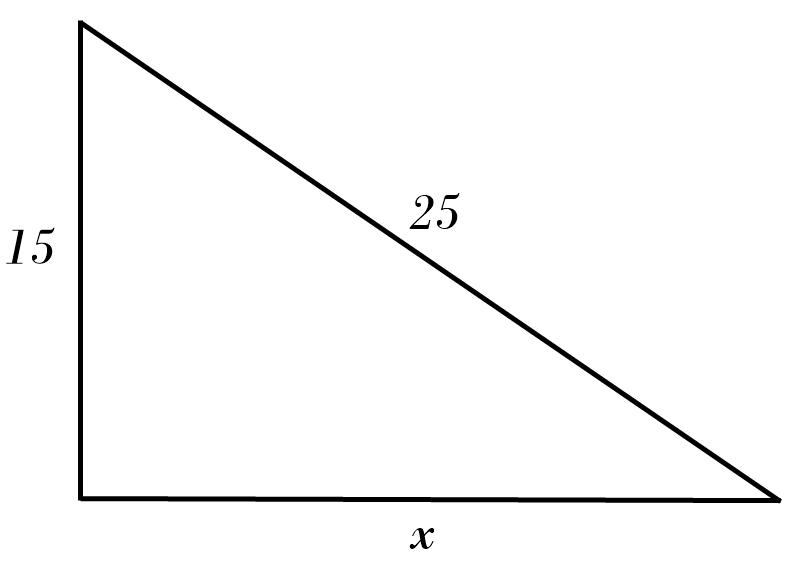
9) \( x = \color{red}{15^2 \ - \ 12^2 = x^2 }\)\( \ \Rightarrow \ x = \color{red}{\sqrt{81} = 9} \)

10) \( x = \color{red}{3^2 \ + \ 4^2 = x^2 }\)\( \ \Rightarrow \ x = \color{red}{\sqrt{25} = 5} \)

The Pythagorean Theorem Practice Quiz