How to Find the Area of Squares, Rectangles, and Parallelograms
Read,5 minutes
What is the Parallelogram’s Area?
A parallelogram’s area is the space bounded by the parallelogram in a provided 2-dimension space. As stated earlier, a parallelogram is a particular kind of quadrilateral having \(4\) sides, as well as the pair of opposite sides, are parallel. With a parallelogram, the opposite sides are an equal length and the opposite angles are also an equal measure. Because the rectangle and the parallelogram have properties that are similar, the rectangular’ s area equals the parallelogram’s area.
Ways to Calculate a Parallelogram’s Area
Step one: Note down this formula: \(A \ = \ bh\). \(A\) stands for the area, while \(b\) stands for the parallelogram’s length, and \(h\) stands for the parallelogram’s height.
Step two: Find the parallelogram’s base. The base equals the length of the bottom side of a parallelogram.
Step three: Find the parallelogram’s height. The height is the length a perpendicular line has to go from the bottom to the top of a parallelogram.
Step four: Multiply the height and the base together.
.png)
What is the Square’s Area?
Squares are closed 2-dimensional shapes having \(4\) equal sides as well as \(4\) equal angles. The square’s \(4\) sides create the \(4\) angles at the vertices. The total of the full length of the sides of a square is the perimeter, as well as the full space the square occupies, is the square’s area. It’s a quadrilateral with these properties.
- Its opposite sides are parallel.
- All \(4\)sides are the same.
- All the angles are \(90°\).
The formula to determine the area of a square when the sides are provided is:
Area of a square \(= \ Side \times Side \ = \ s^2\)
.png)
A square’s area may additionally be calculated via the assistance of the square’s diagonal. The formula utilized for finding a square’s area if the diagonal is provided is:
Area of a square using diagonals \(= \ \frac{Diagonal^2}{2}\)
What is the Rectangle’s area?
The area of a rectangle is calculated via the sides. Usually, a rectangle’s area equals the product of its length and width. The rectangle’s perimeter, though, equals the total of all its \(4\) sides. So, the rectangle’s area is described as the area encompassed by the perimeter. Rectangles are quadrilaterals whose opposite sides are equal and parallel to one another. Because rectangles have \(4\) sides, there are also \(4\) angles. All the rectangle’s angles equal \(90\) degrees; so, all the rectangle’s angles are right angles.
Formula for Determining the Area of a Rectangle
A rectangle’s area is determined in units via multiplying the width (or breadth) by the rectangle’s length.
Area of a Rectangle \(A \ = \ l \times b\)
.png)
Follow these steps to determine the area:
- Step one: Write down the length and width dimensions using provided data
- Step two: Multiply the values of the length and width
- Step three: Write down the solution in square units
Free printable Worksheets
Exercises for Area of Squares, Rectangles, and Parallelograms
1)
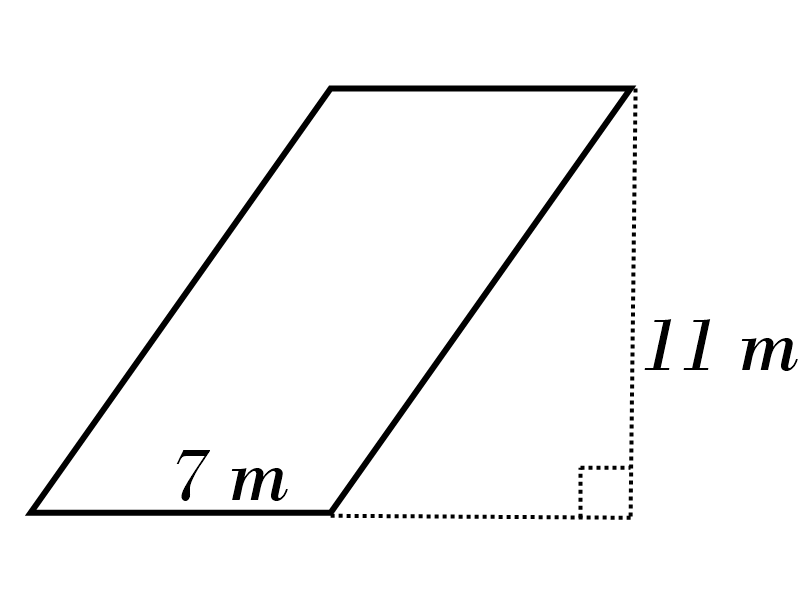
2)
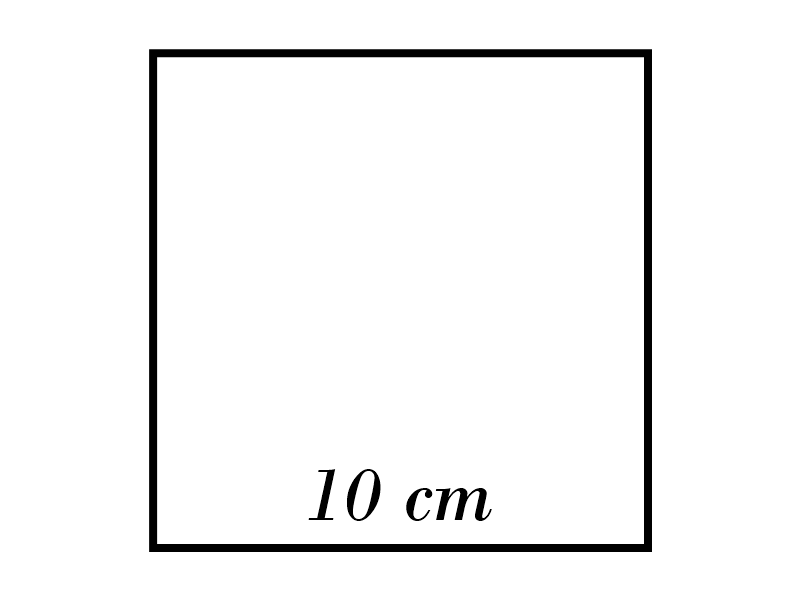
3)
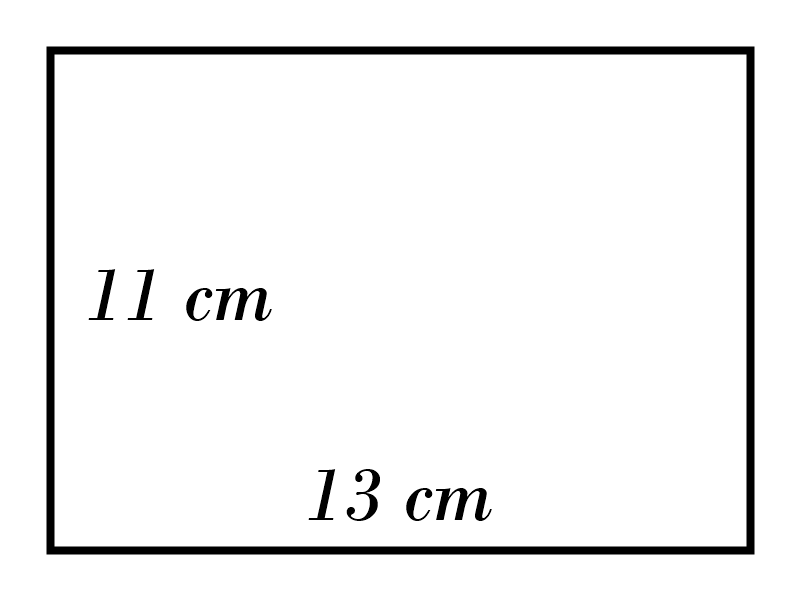
4)
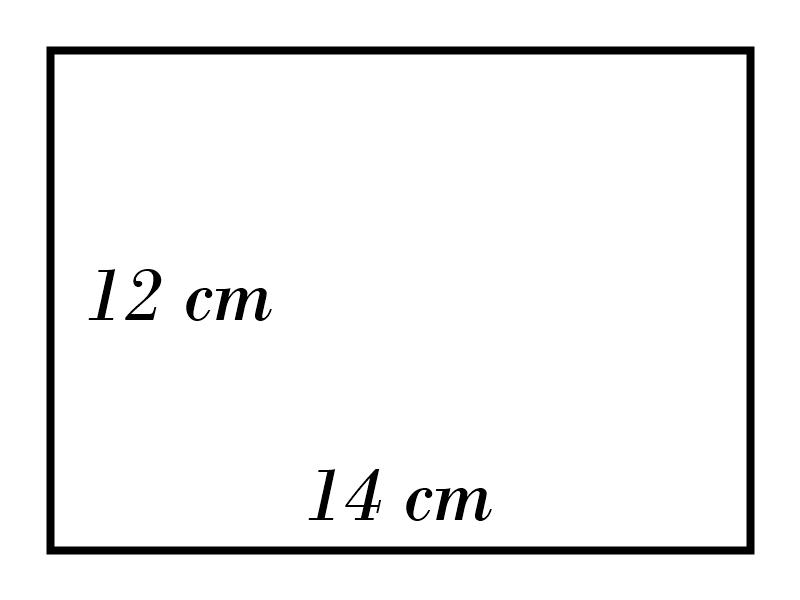
5)
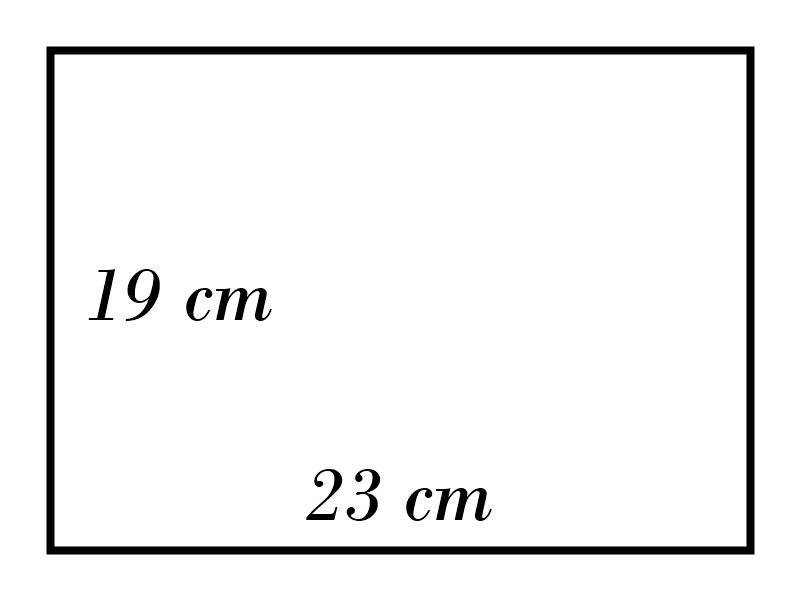
6)
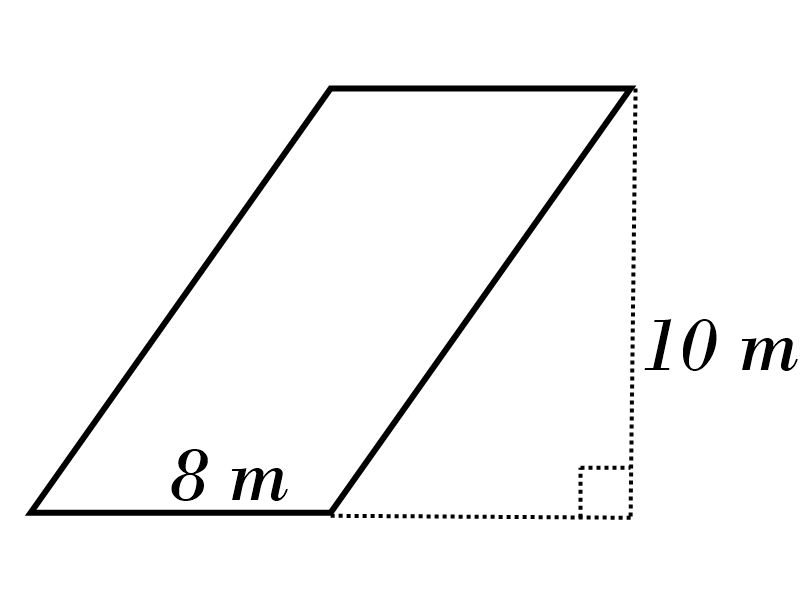
7)
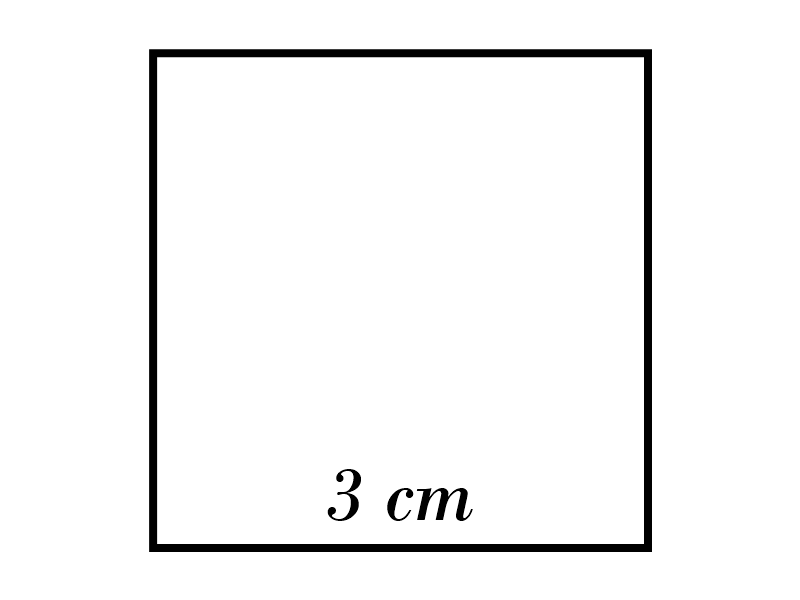
8)
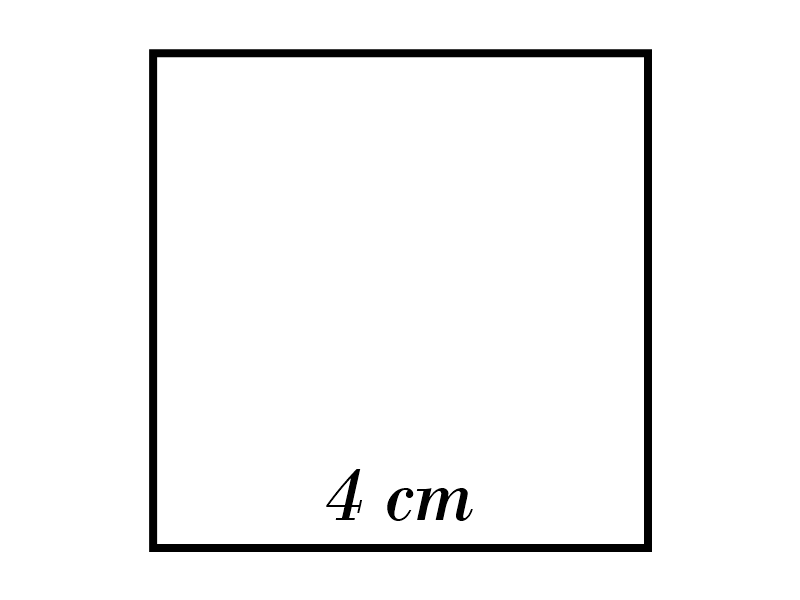
9)
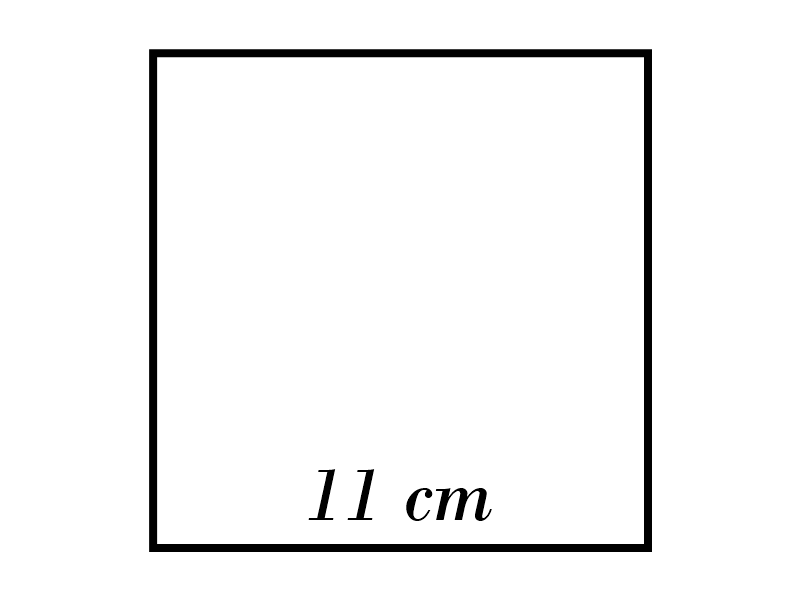
10)
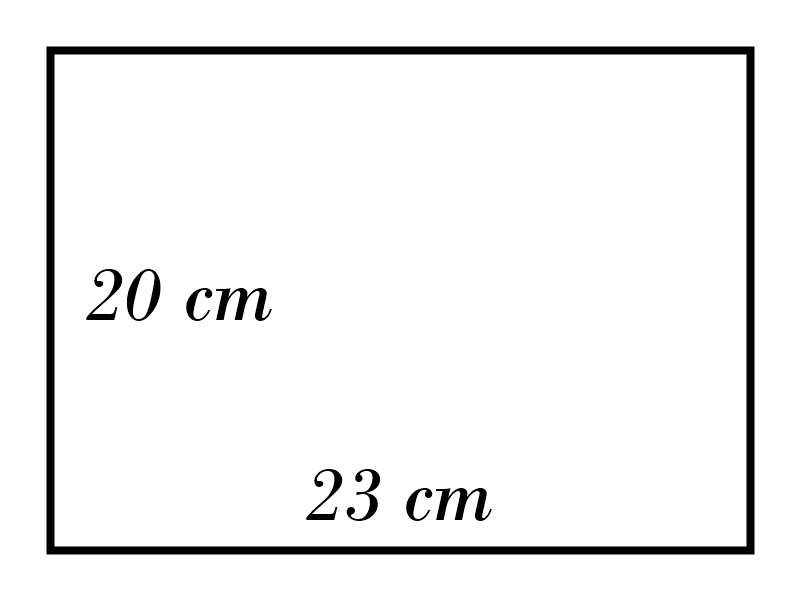
1) \( \ \color{red}{77 \ m} \)

2) \( \ \color{red}{100 \ cm^2} \)

3) \( \ \color{red}{143 \ cm^2} \)

4) \( \ \color{red}{168 \ cm^2} \)

5) \( \ \color{red}{437 \ cm^2} \)

6) \( \ \color{red}{80 \ m^2} \)

7) \( \ \color{red}{9 \ cm^2} \)

8) \( \ \color{red}{16 \ cm^2} \)

9) \( \ \color{red}{121 \ cm^2} \)

10) \( \ \color{red}{460 \ cm^2} \)

Area of Squares, Rectangles, and Parallelograms Practice Quiz