How to Find Volume and Surface Area of Pyramids and Cone
Read,5 minutes
PYRAMIDS
A pyramid is a solid shape with a polygonal base and triangular sides that meet at a point called the "apex." The name of a pyramid comes from the shape of its ground. Most pyramids have a base that is a square or another regular polygon. This makes all sides of the pyramid the same shape, an isosceles triangle. The height is the straight line distance from the top to the middle of the bottom. The edge length and the slant height are other ways to measure pyramids. The edge length is the length of the sides of the triangles, and the slant height is the height of the triangles.
.png)
Pyramid's volume
Generally, the volume of a pyramid with a base of area \(B\) and height \(h\) is: \(V \ = \ \frac{1}{3} \ B \ h\)
If the base is a square with sides that are each \(s\) long, then the volume is: \(V \ = \ \frac{1}{3} \ s^2 \ h\)
The volume of a pyramid is the same as that of a prism with the same base and height.
Pyramid's Lateral Surface Area
If the base of a pyramid is a regular polygon with \(n\) sides, the length of each \(s\), and the slant height is 𝑙, then:
\(LSA \ = \ \frac{1}{2} \ n \ s \ l\)
If the square base, then: \(LSA \ = \ 2 \ s \ l\) \((n \ = \ 4)\)
Pyramid's Total Surface Area
For the total area \((TSA)\), you simply put together both the base and lateral surface area:
\(TSA \ = \ LSA \ + \ B\)
If the square base, then: \(TSA \ = \ 2 \ s \ l \ + \ s^2\)
CONES
Cone is a pyramid with a circular base.
.png)
You might be able to figure out a cone's height \(h\) (the distance from the top perpendicular to the base) or its slant height \(l\). (the length from the apex to the edge of the circular base). Note that the height, the radius, and the slant height form a right triangle, with the slant height as the hypotenuse. With the Pythagorean theorem, we can determine that the following things are the same.
The slant height \(l\), height \(h\), and radius \(r\) of a cone are related as follows:
- \(l \ = \ \sqrt{r^2 \ + \ h^2}\)
- \(h \ = \ \sqrt{l^2 \ - \ r^2}\)
- \(r \ = \ \sqrt{l^2 \ - \ h^2}\)
Cone's volume
The volume of a cone is equal to one-third of the volume of a cylinder that has the same base and height. This is similar to the way that the volume of a pyramid is equal to one-third of the volume of a prism that has the same base and height.
A cone's volume is equal to one-third of the product of its base area with radius \(r\) and its height \(h\).
\(V \ = \ \frac{1}{3} \ πr^2 \ h\)
Cone's Surface Area
\(LSA \ = \ πrl\)
\(TSA \ = \ LSA \ + \ πr^2 \ = \ πrl \ + \ πr^2\)
Free printable Worksheets
Exercises for Pyramids and Cone
1)
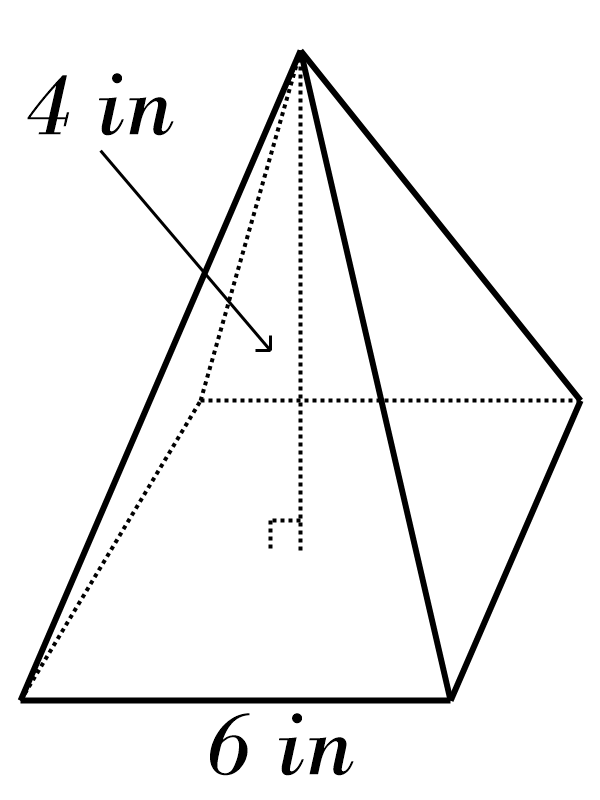
2)
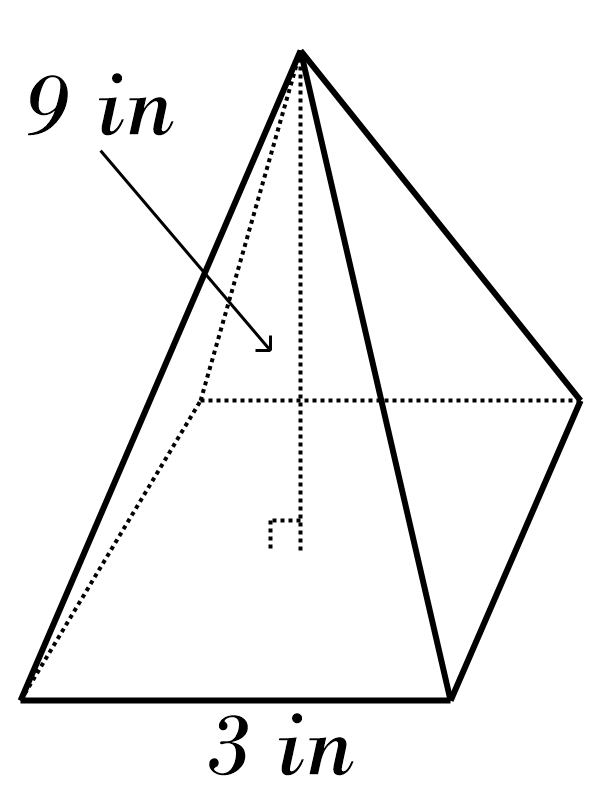
3)
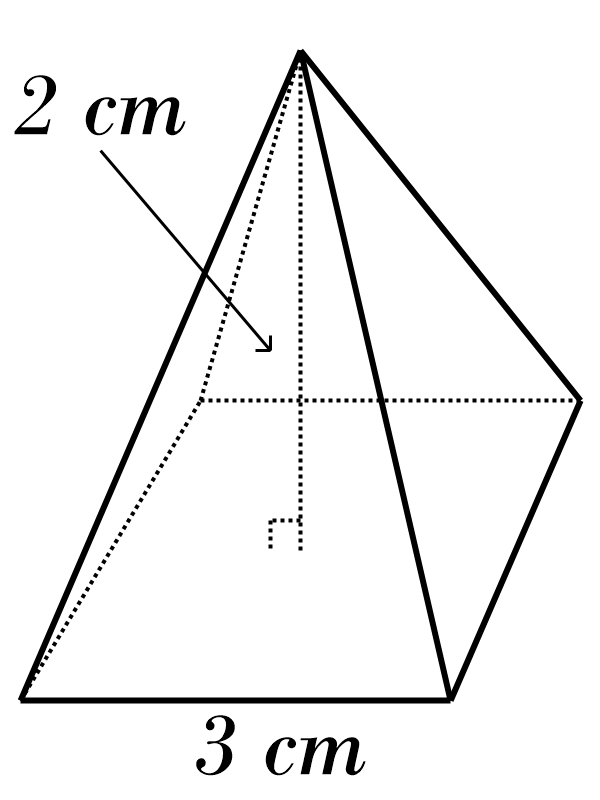
4)
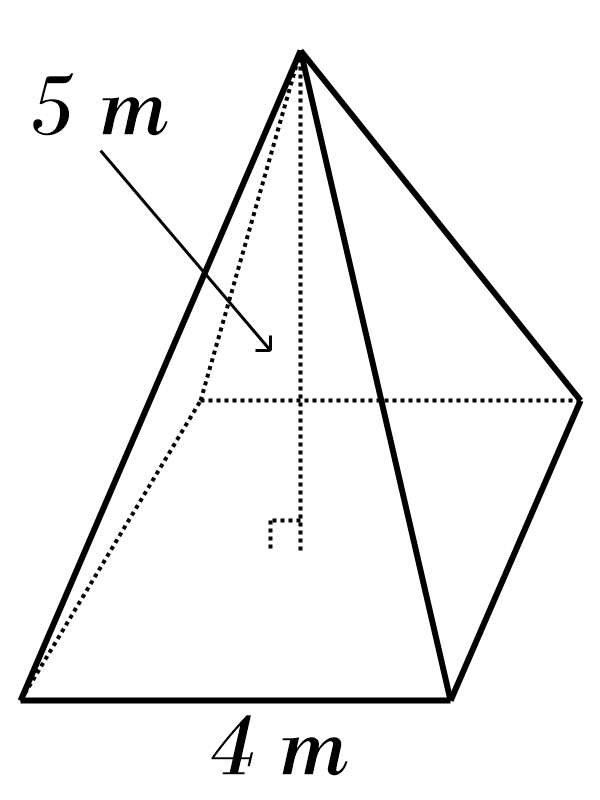
5)
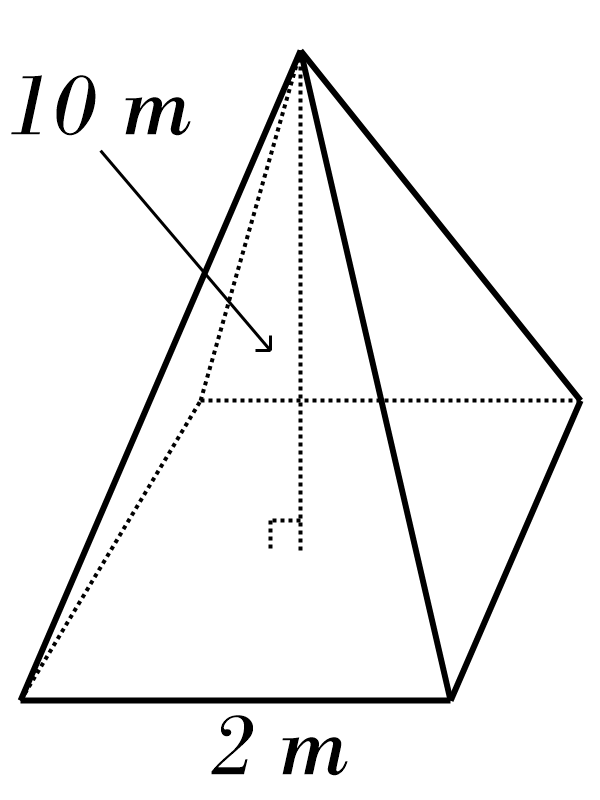
6)
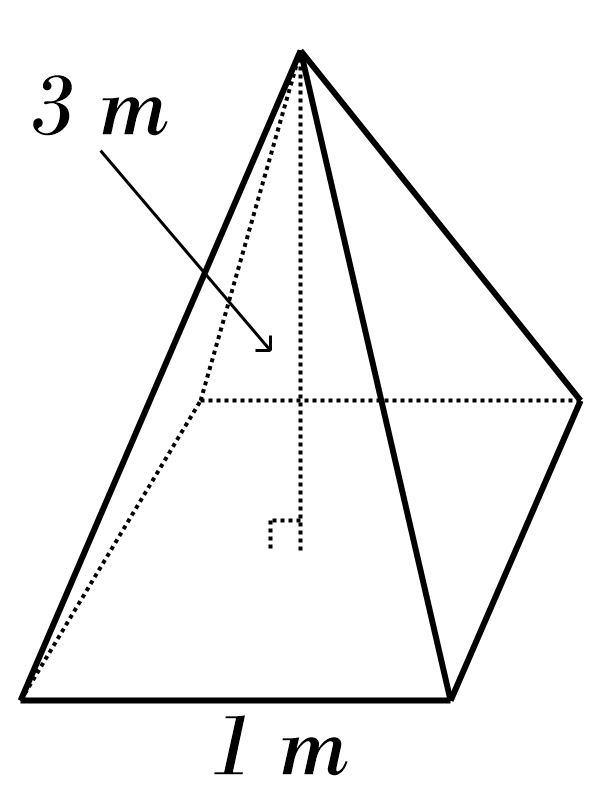
7)
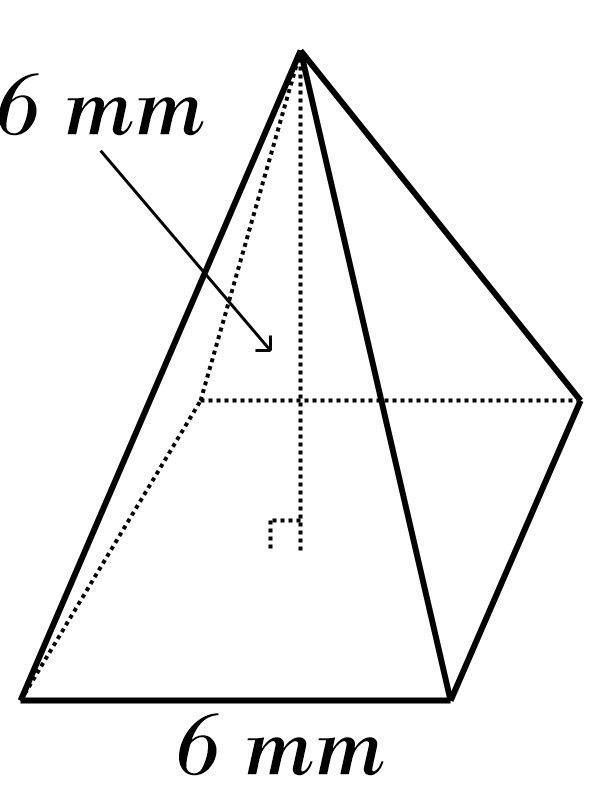
8)
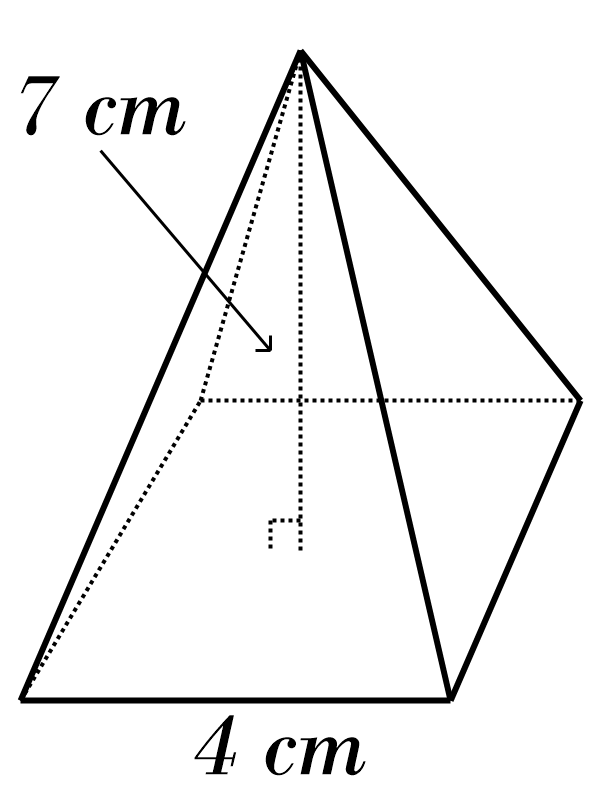
9)
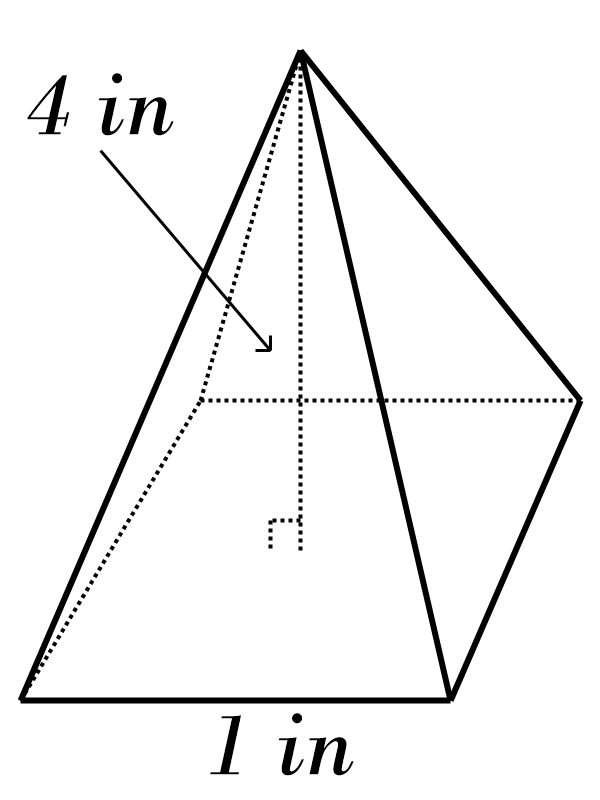
10)
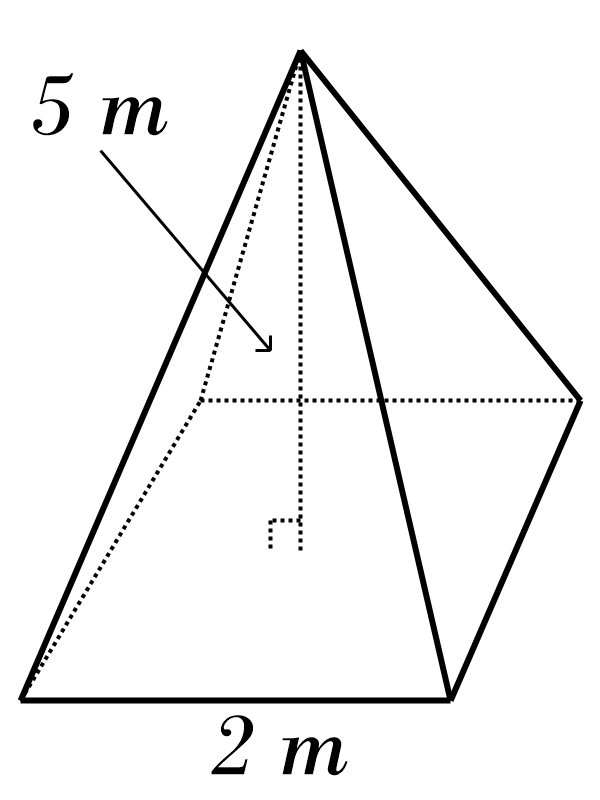
Pyramids and Cone Practice Quiz