How to Find the Surface Area of a Rectangular Prism

How to Find the Surface Area of a Rectangular Prism

 Read,3 minutes

A prism is a polyhedron having two bases that are parallel to one another. A rectangular prism has two similar rectangular bases and four rectangular faces. The rectangular prism's surface area equals the sum of the areas of its side faces and rectangular bases. Square units are used to measure the surface area of a rectangular prism.

Here is an example of a rectangular prism:

Rectangle_Prism1

The formula for the surface area of a rectangular prism is, \(2(bl \ + \ lh \ + \ hb)\)

Where,

  • \(b\) is the length of the base of the prism.
  • \(l\) is the width of the base of the prism.
  • \(h\) is the height of the square prism.

Example:

Find the surface area of a prism with a base of \(6\) cm, a height of \(14\) cm, and a side of \(3\) cm.

Solution:
Given, \(b \ = \ 6\) cm, \(l \ = \ 3\) cm, \(h \ = \ 14\) cm
Surface area of rectangle prism \(= \ 2(bl \ + \ lh \ + \ hb) \ = \ 2(18 \ + \ 42 \ + \ 84) \ = \ 288\) cm\(^2\)

Free printable Worksheets

Exercises for Surface Area of a Rectangle Prism

1) 
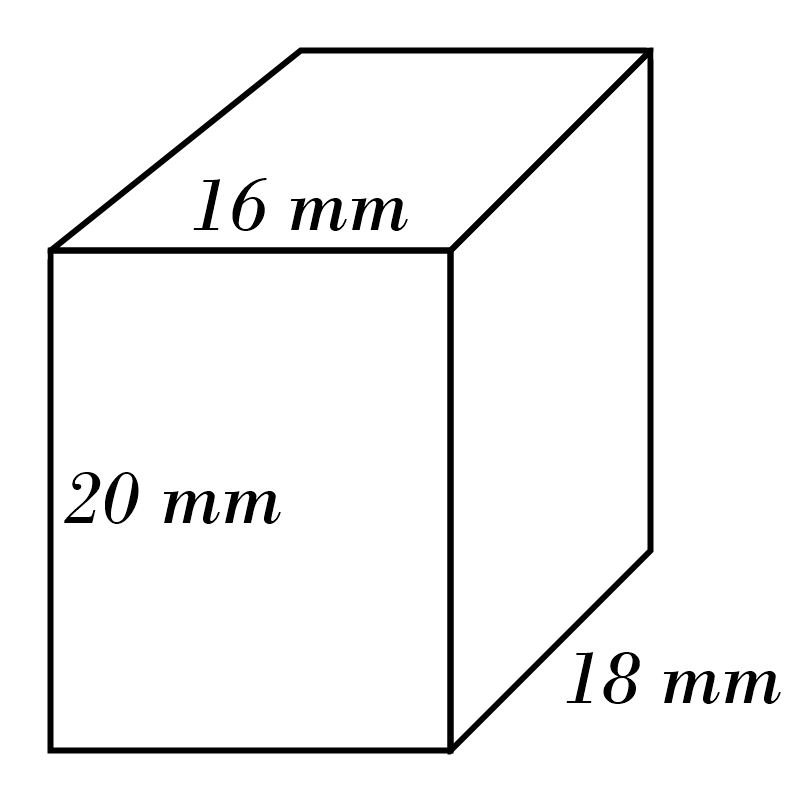
Rectangular Prism1

2) 
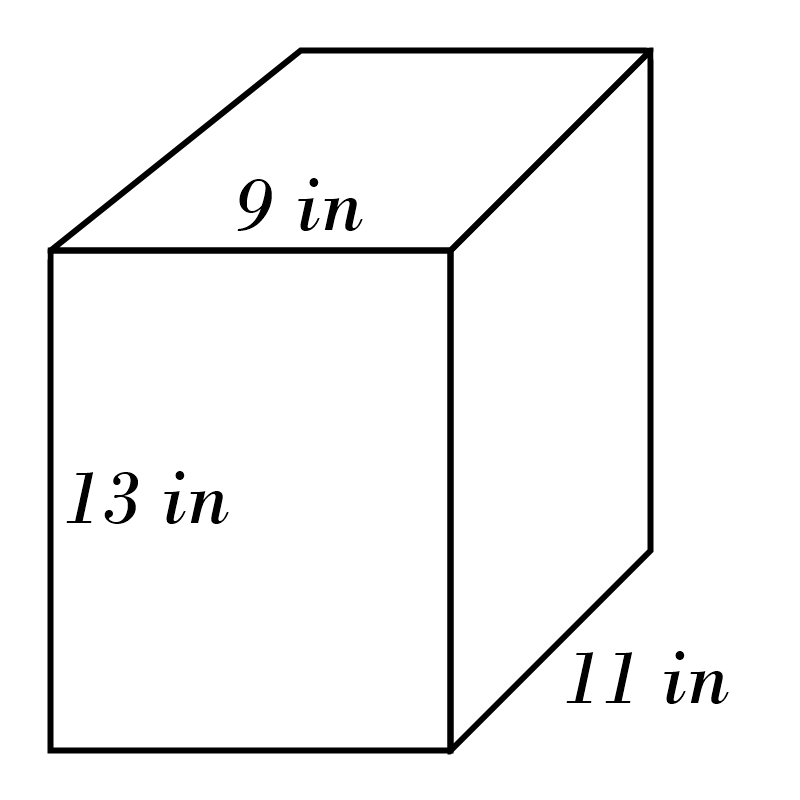
Rectangular Prism2

3) 
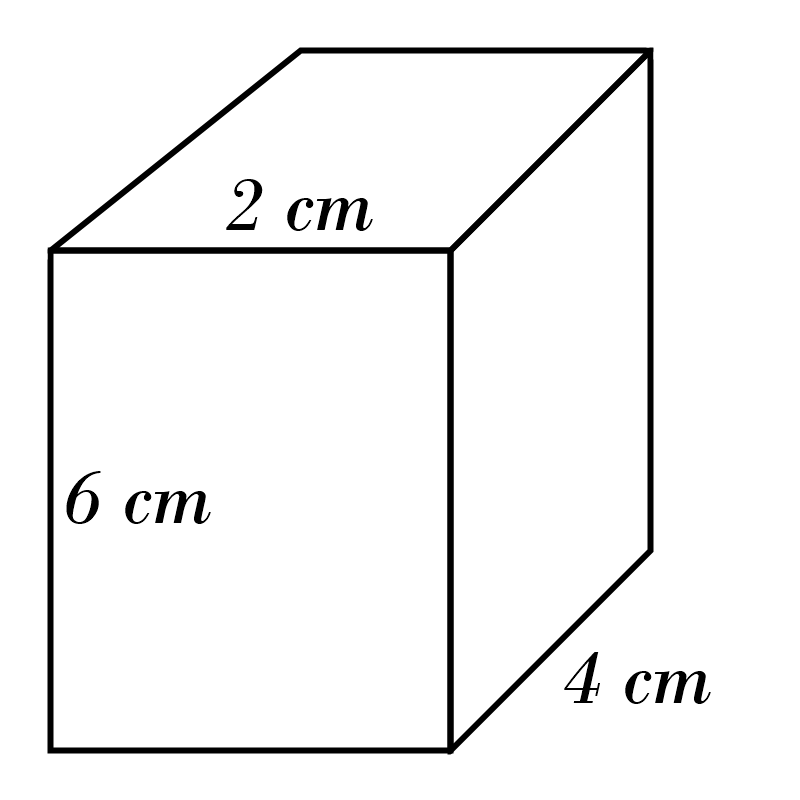
Rectangular Prism3

4) 
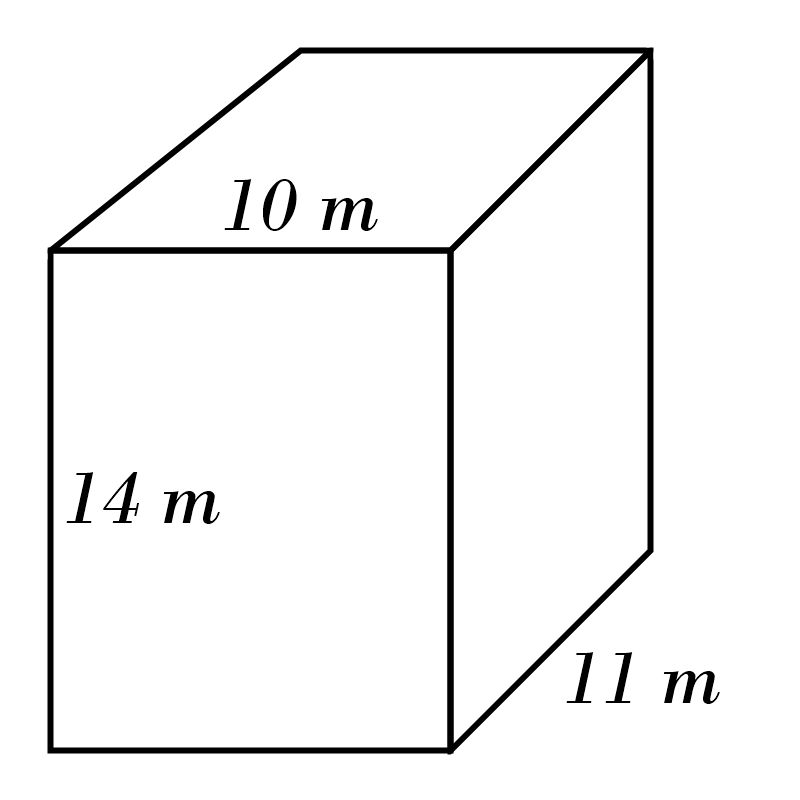
Rectangular Prism4

5) 
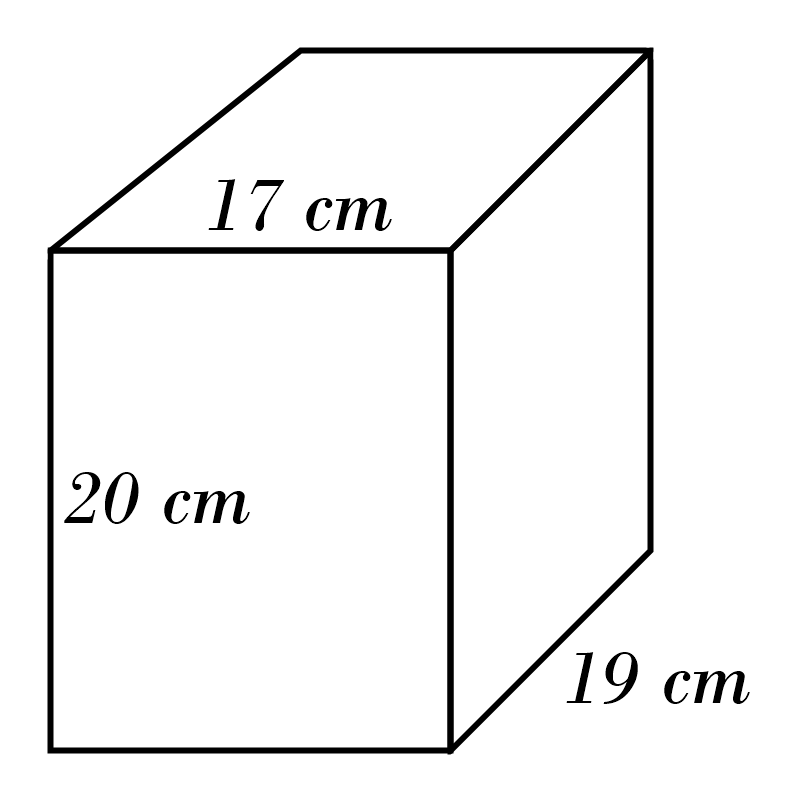
Rectangular Prism5

6) 
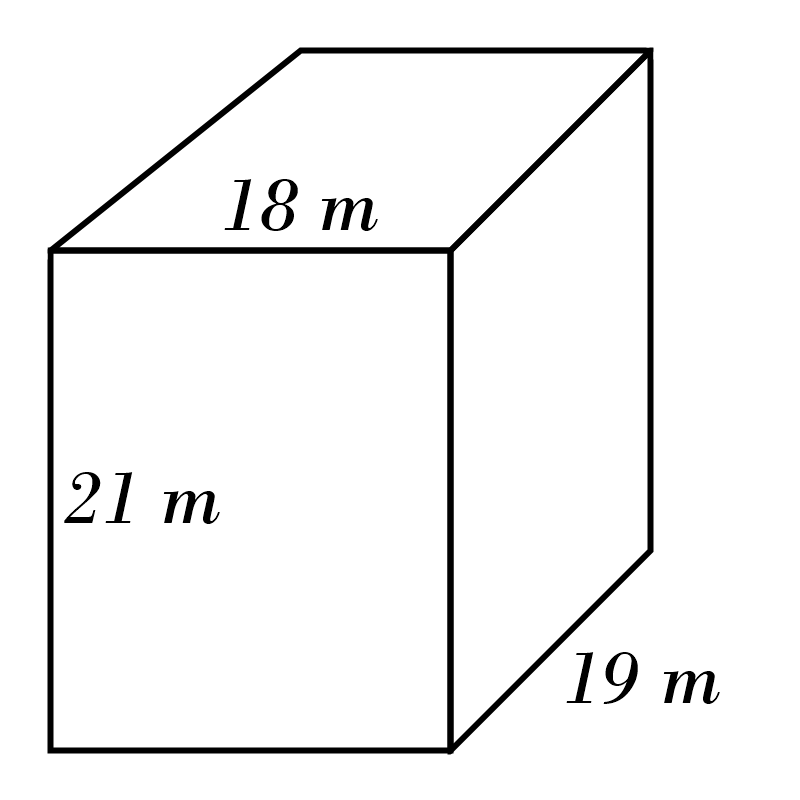
Rectangular Prism6

7) 
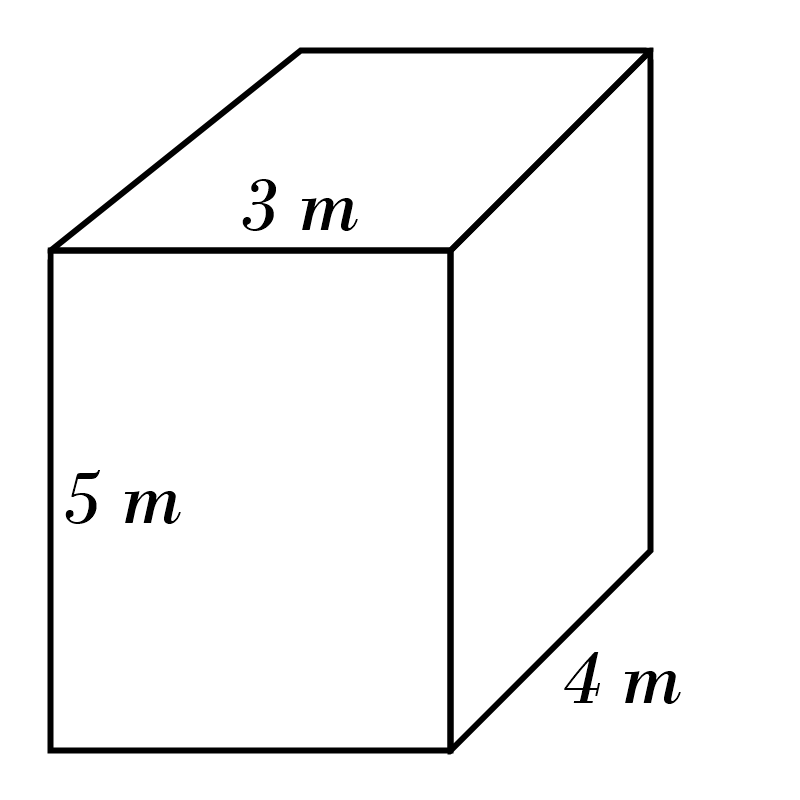
Rectangular Prism7

8) 
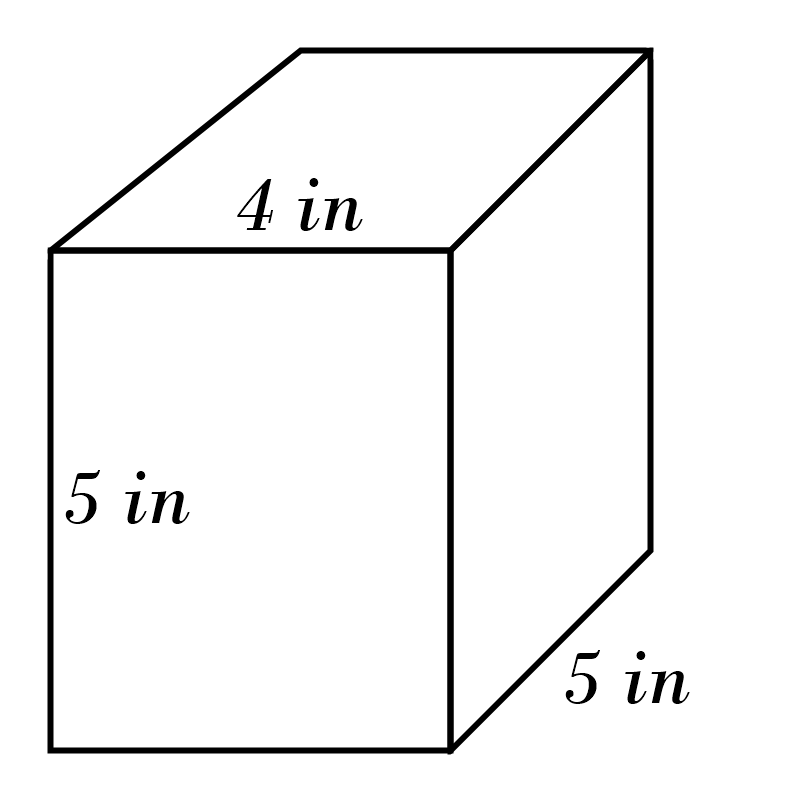
Rectangular Prism8

9) 
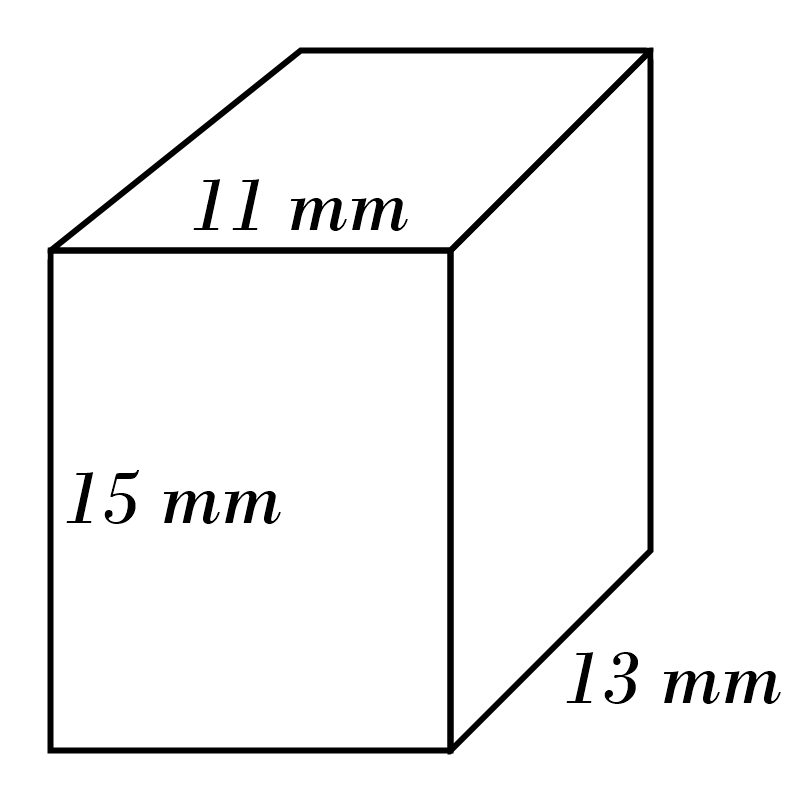
Rectangular Prism9

10) 
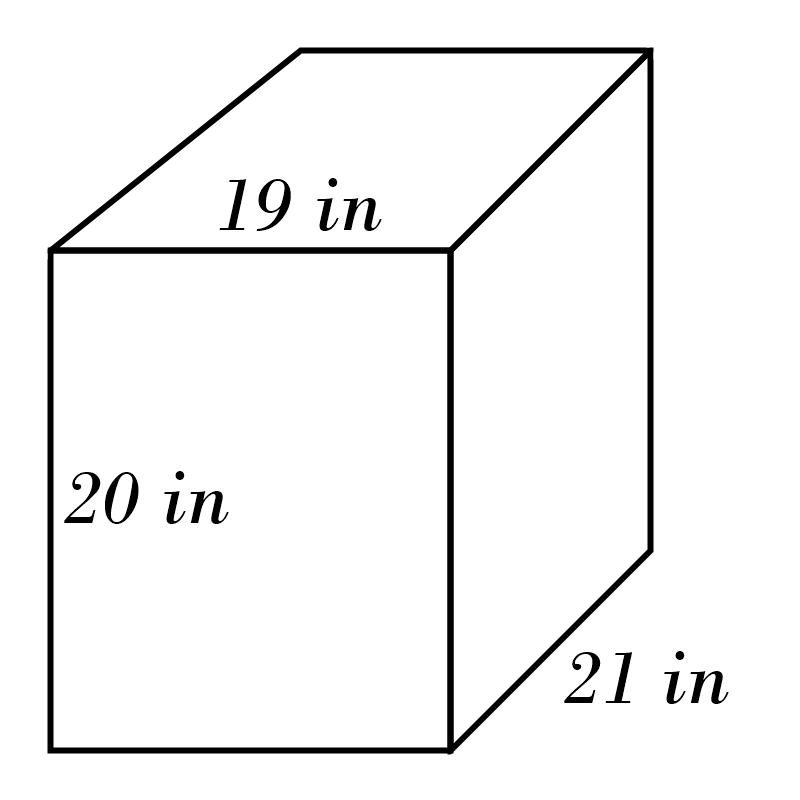
Rectangular Prism0

 
1) \(1936 \) mm\(^2\)
Rectangular Prism1
2) \(718 \) in\(^2\)
Rectangular Prism2
3) \(88 \) cm\(^2\)
Rectangular Prism3
4) \(808 \) m\(^2\)
Rectangular Prism4
5) \(2086 \) cm\(^2\)
Rectangular Prism5
6) \(2238 \) m\(^2\)
Rectangular Prism6
7) \(94 \) m\(^2\)
Rectangular Prism7
8) \(130 \) in\(^2\)
Rectangular Prism8
9) \(1006 \) mm\(^2\)
Rectangular Prism9
10) \(2398 \) in\(^2\)
Rectangular Prism0

Surface Area of a Rectangle Prism Practice Quiz