How to Find the Volume of a Cube

How to Find the Volume of a Cube

 Read,4 minutes

What Is A Cube?

A cube is a three-dimensional solid that has six square faces that are the same and meet at right angles, eight corners, and twelve sides that are all the same length. One of the 5 Platonic Solids is a cube, also known as a hexahedron.
There are three sides to a cube:

• Length is usually considered the bigger of the "flat" measurements.
• Width is usually the shorter of the two "flat" measurements.
• Height or depth is the dimension that gives a shape three-dimensionality.

How to Find the Volume of a Cube

The length of each edge of the cube is the same.

$V \ = \ w.l.h$, width $=$ length $=$ height $= \ S$

Simplify the formula so:

$V \ = \ s^3$

How to Calculate Volume Based on Area

Here's another problem to solve. What if the area of one side of a cube is given? Can you figure out the volume from that?

Yes, the area of a face is equal to the $length \times Width$ of the face. Once you know how long or wide something is, you can use the volume formula:

• Find the square root of the given area measurement. This will tell you the length of any side.
• Use the volume formula to figure out how big the volume is $V \ = \ s^3$.

Example 1:

Find the cube's volume if each side is $7$ cm long.

Solution:

Given that each side of the cube is $7$ cm long. We know that a cube's volume is equal to (its sides' length)$^3$.

So, the volume, $V$, is equal to $(7 \ cm)^3$ $⇒ \ V \ = \ 343 \ cm^3$

Example 2:

If one side of a cube has an area of $187.69$, what is the cube's volume?

Solution:

Given that one side of the cube has an area of $187.69$, We know that the area of one side of a cube is equal to the length of its sides squared.

So, the length of any side, S, equals: $S \ = \ \sqrt{187.69} \ = \ 13.7$

So, Volume, $= \ (13.7)^2$

Free printable Worksheets

Exercises for Volume of Cubes

1) 

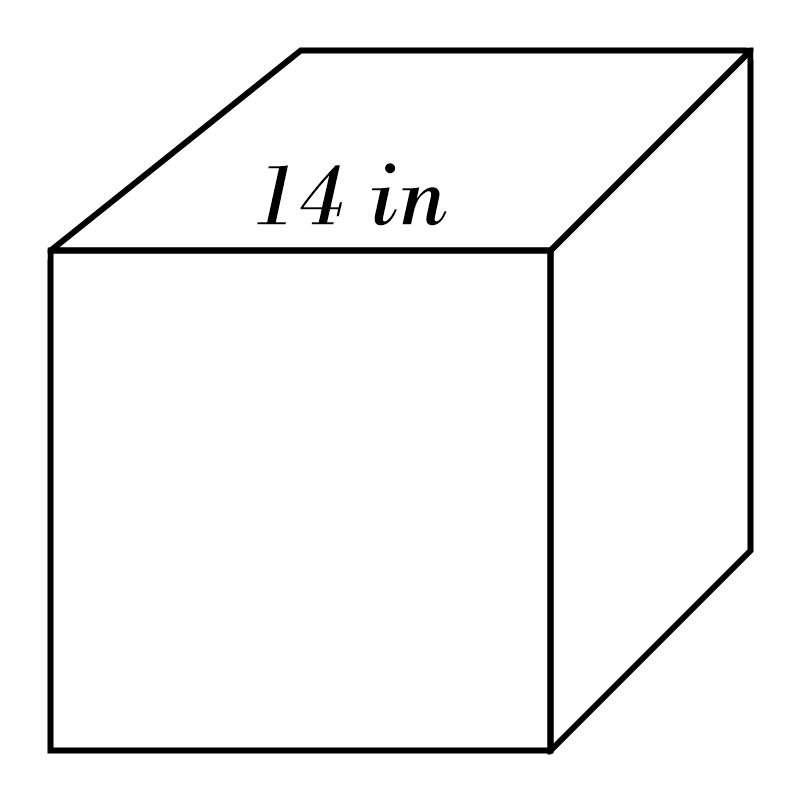
2) 

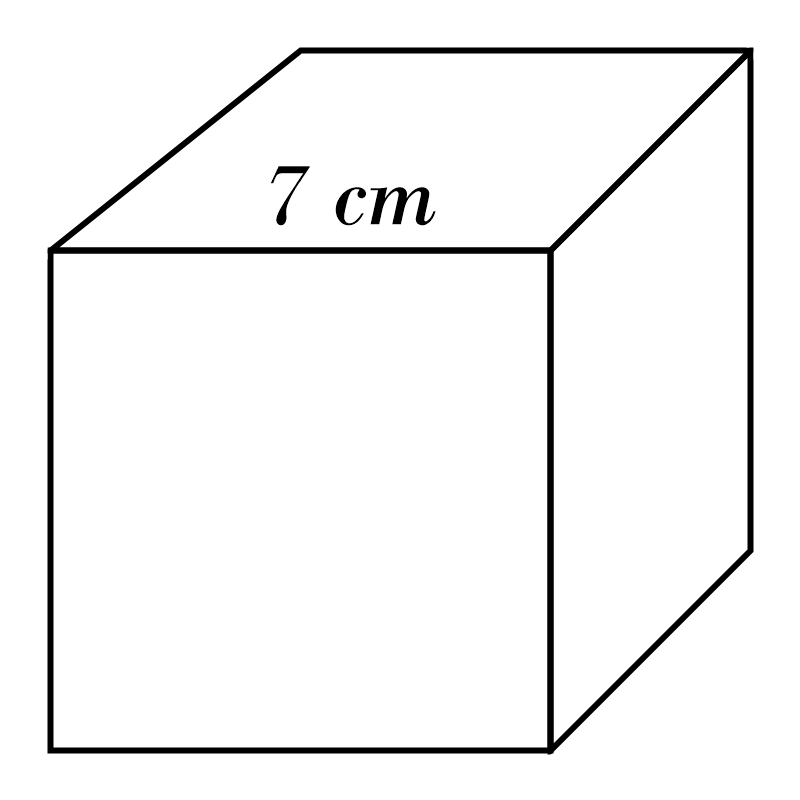
3) 

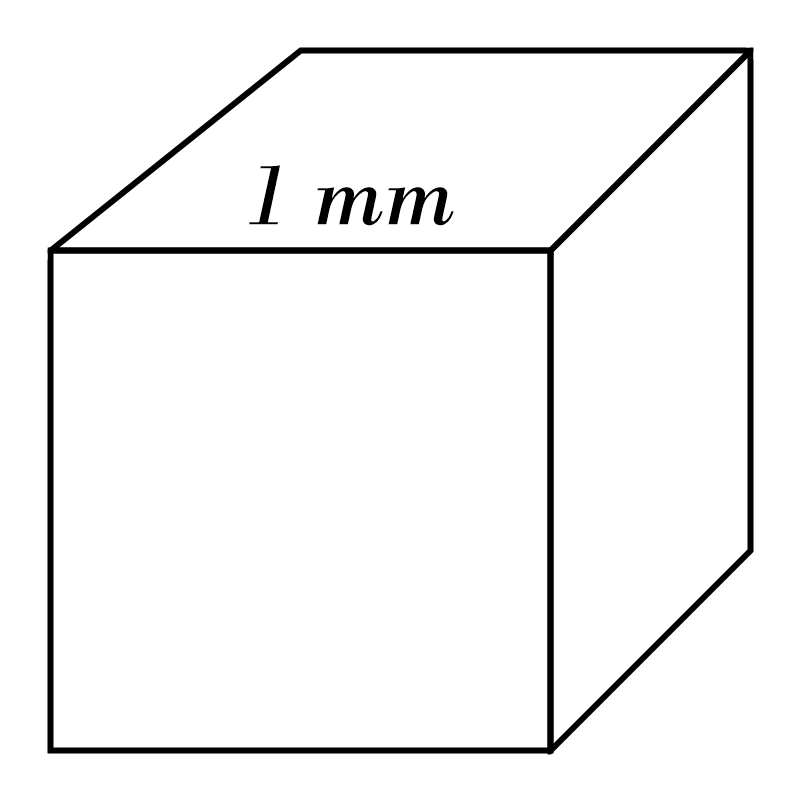
4) 

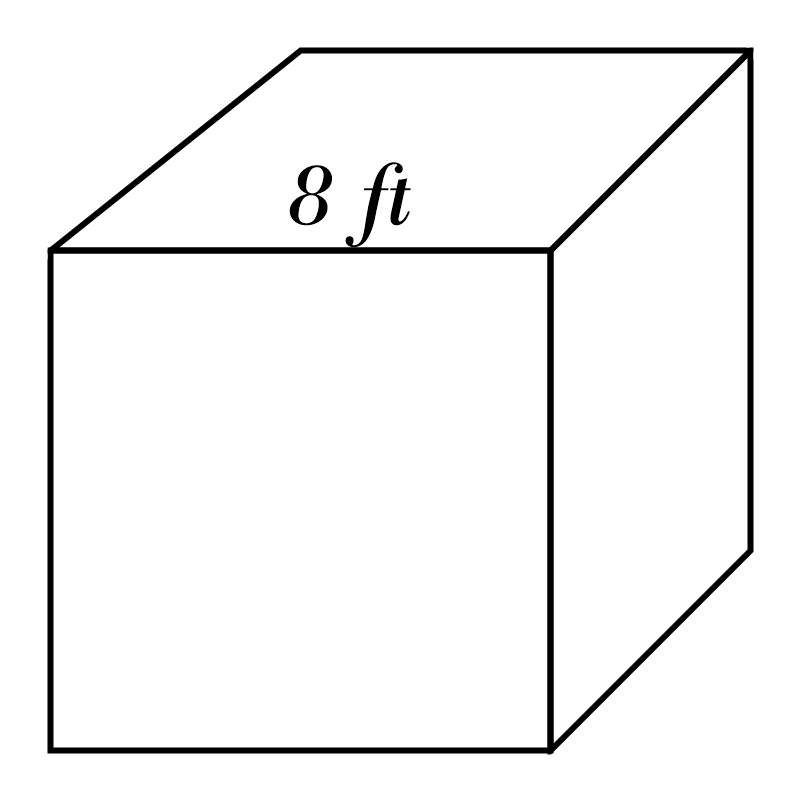
5) 

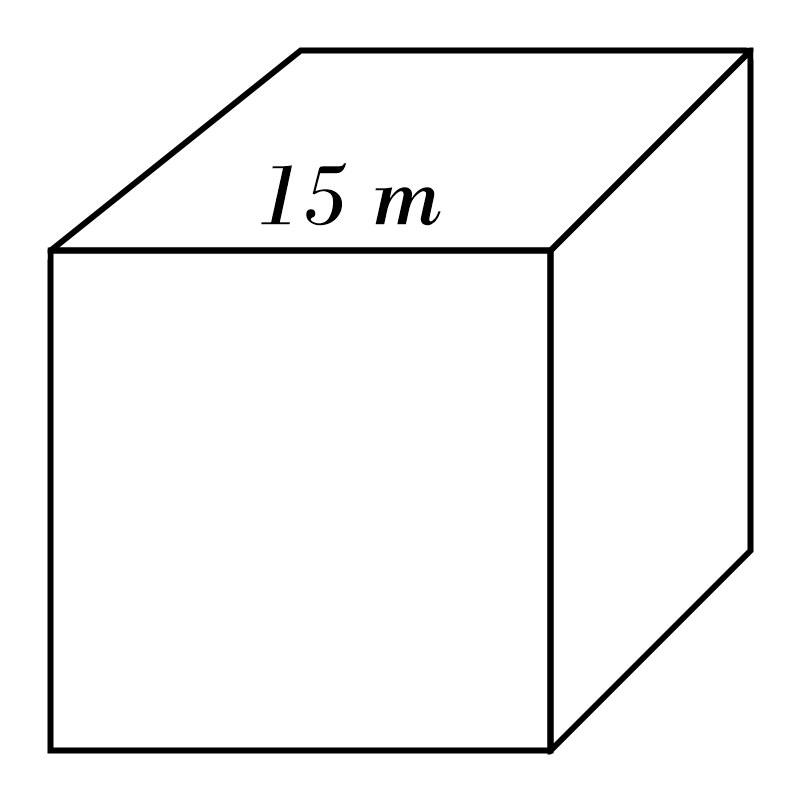
6) 

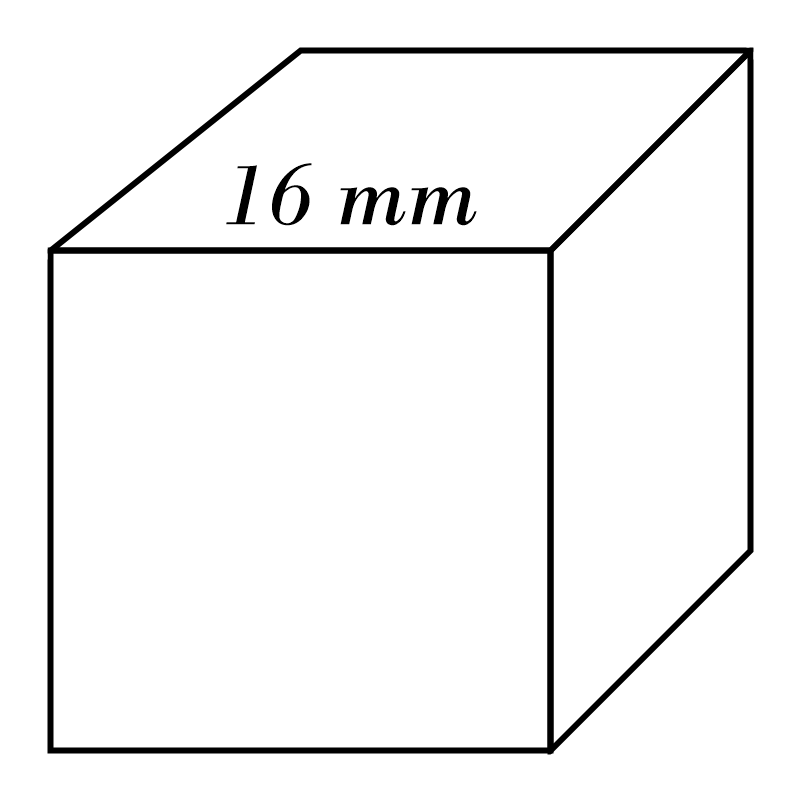
7) 

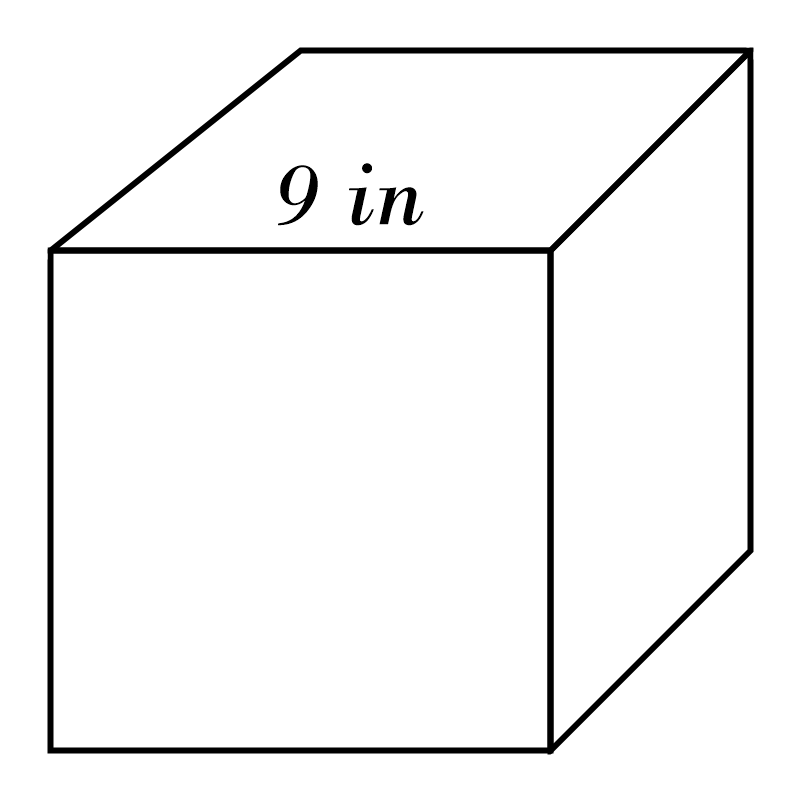
8) 

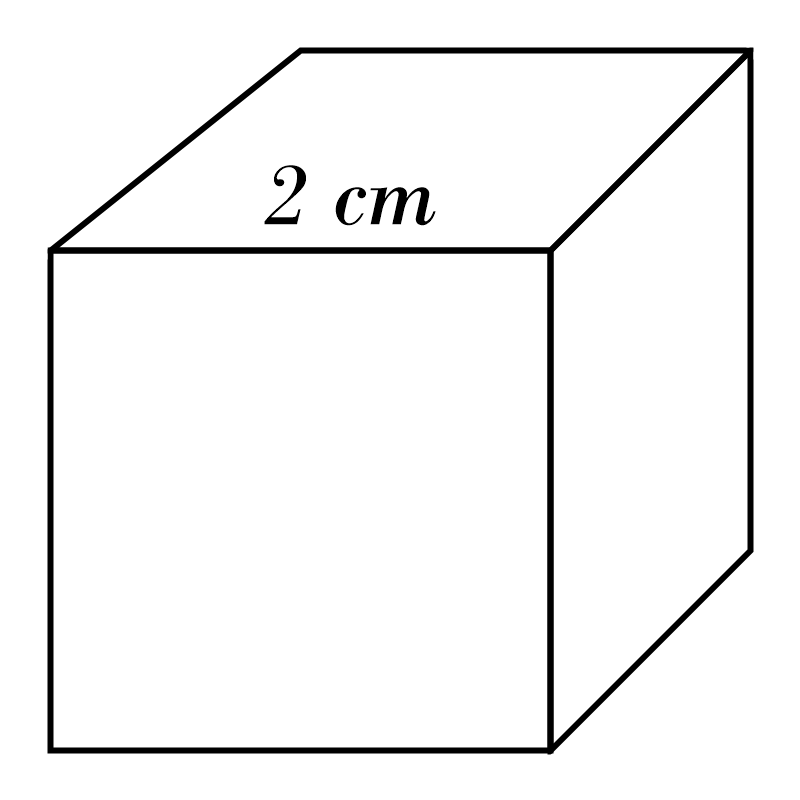
9) 

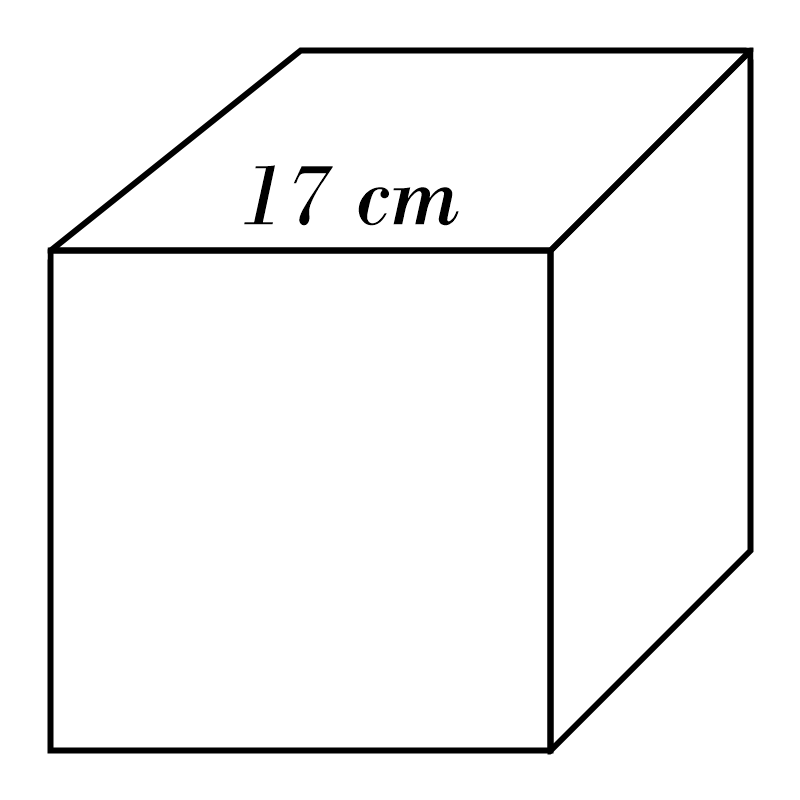
10) 

 

Answers

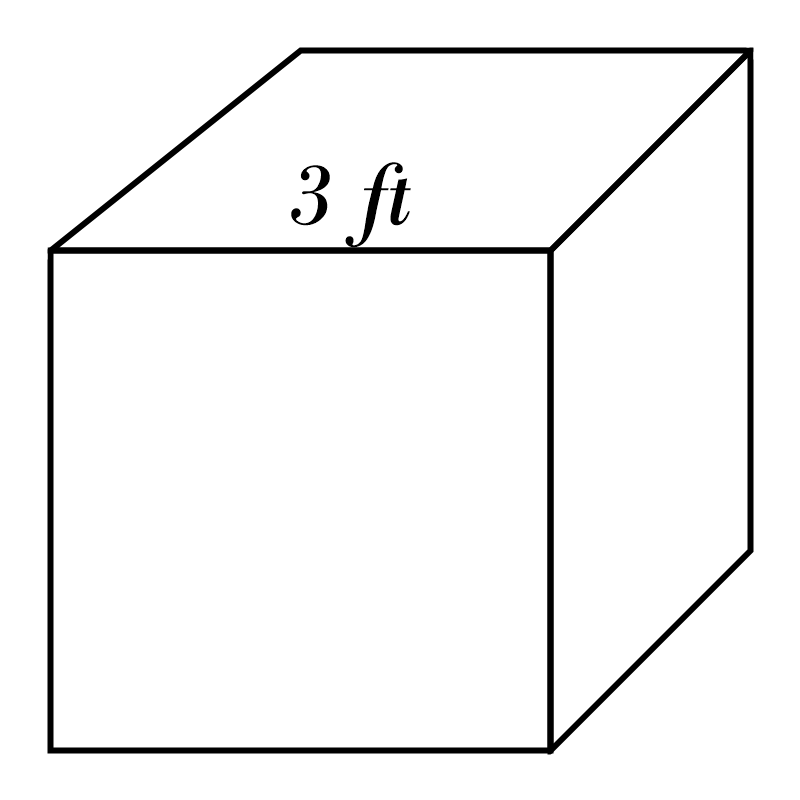
1) $\color{red}{2744}$ in$^3$

2) $\color{red}{343}$ cm$^3$

3) $\color{red}{1}$ mm$^3$

4) $\color{red}{512}$ ft$^3$

5) $\color{red}{3375}$ m$^3$

6) $\color{red}{4096}$ mm$^3$

7) $\color{red}{729}$ in$^3$

8) $\color{red}{8}$ cm$^3$

9) $\color{red}{4913}$ cm$^3$

10) $\color{red}{27}$ ft$^3$

Volume of Cubes Practice Quiz

Quiz 1 Quiz 2

More Solid Figures courses

• How to Find the Volume of a Rectangular Prism
• How to Find the Volume of a Cylinder
• How to Find the Surface Area of a Cylinder
• How to Find the Surface Area of a Rectangular Prism
• How to Find Volume and Surface Area of Cubes
• How to Find the Volume of a Cube
• How to Find Volume and Surface Area of Pyramids and Cone