
How to Find the Volume of a Rectangular Prism
Read,5 minutes
The volume of Rectangular Prisms
A prism is a polyhedron with flat sides and bases of the same length. It is a solid object with flat sides, the same ends, and a cross-section that is the same length as the object. In Geometry, we will learn about the different prisms, such as a triangular prism, a pentagonal prism, and a hexagonal prism. Because it is a three-dimensional figure, it has both a surface area and a volume.
How much space does a prism take up?
The volume of a prism is the amount of space the three-dimensional object takes up as a whole. In math, it is equal to the product of the length and the area of the base. Therefore,
The volume of a prism \(=\) Base Area \(\times\) Length
A three-dimensional object's volume is expressed in cubic units, a measuring unit.
The volume of a rectangle-shaped prism
A rectangular prism has four straight sides and two square bases next to each other. We know that a rectangular prism is cut into a rectangle. The square-shaped prism is also called a "cuboid."
So, here is the formula for figuring out the volume of a rectangular prism:
A rectangular prism has a volume of \(l \times b \times h\) cubed units. Where:
- \(l \ =\) Width of a rectangle's base
- \(b \ =\) length of the base of a rectangular prism
- \(h \ =\) the height of a rectangle
Example:
Find the volume of the rectangle-shaped prism shown below.
.png)
- Step 1: Figure out the rectangular prism's length \((l)\), width \((w)\), and height \((h)\).
Most of the time, the vertical side of a rectangular prism is thought to be its height, so \(h \ = \ 6\) cm. Length is usually believed to be the length of the remaining measurements, so we have \(l \ = \ 5\) cm. and \(w \ = \ 3\) cm.
- Step 2: Use the formula \(V \ = \ l \times w \times h\) to figure out the volume. Don't forget to put the units, units\(^3\).
To get the volume, we need to multiply the length, width, and height.
\(V \ = \ 5 \times 3 \times 6 \ = \ 90\)
The volume is \(90\) cm\(^3\).
Free printable Worksheets
Exercises for Volume of Rectangle Prisms
1)
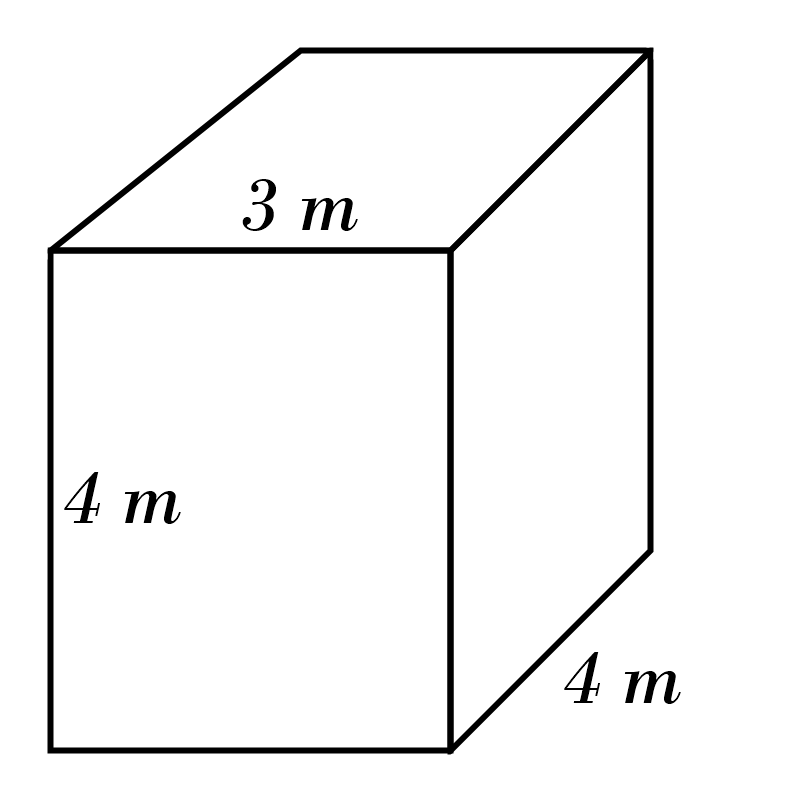
2)
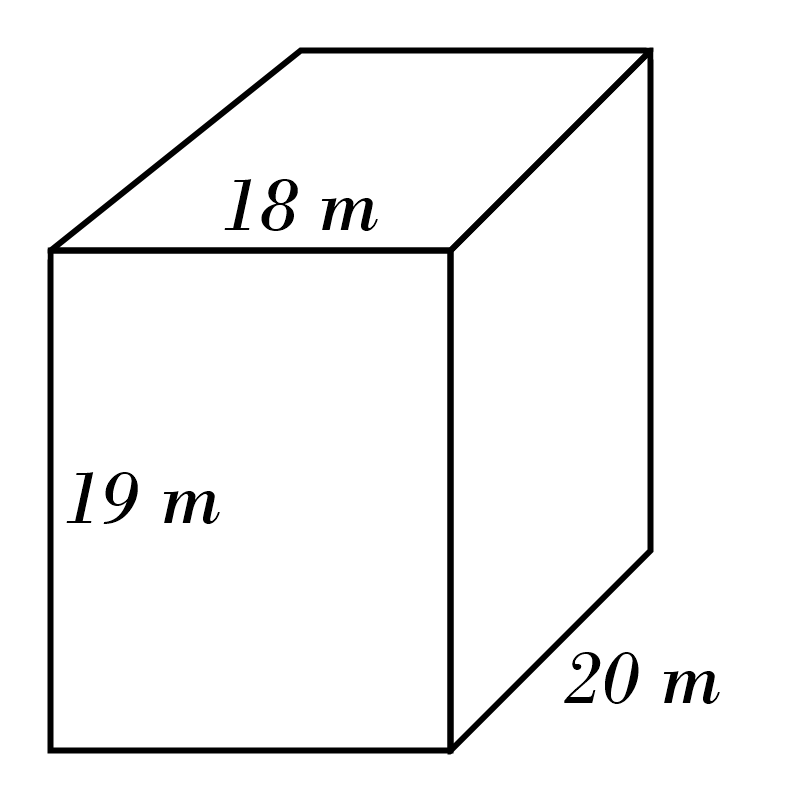
3)
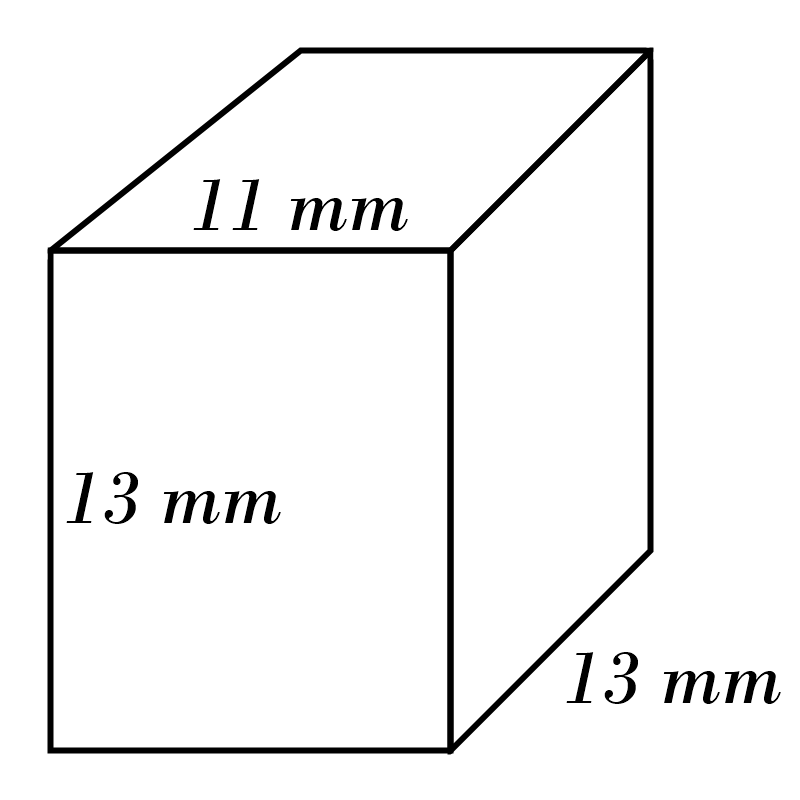
4)
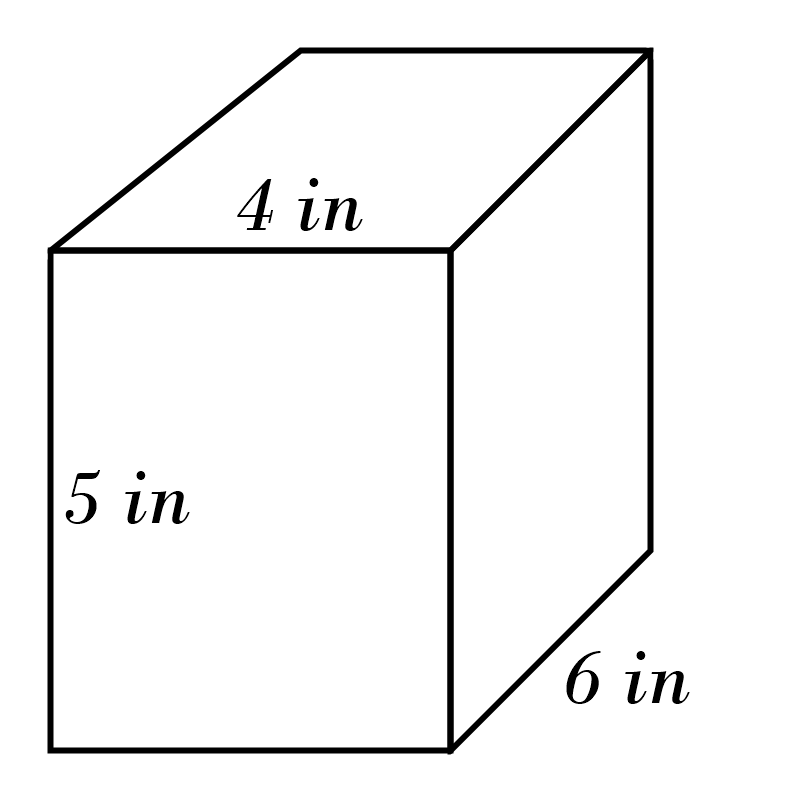
5)
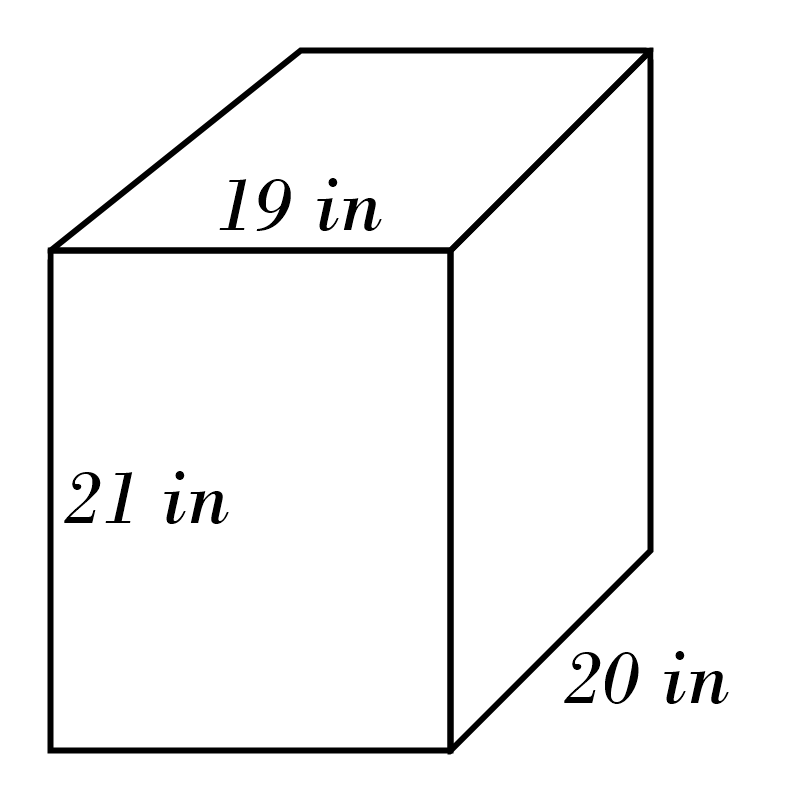
6)
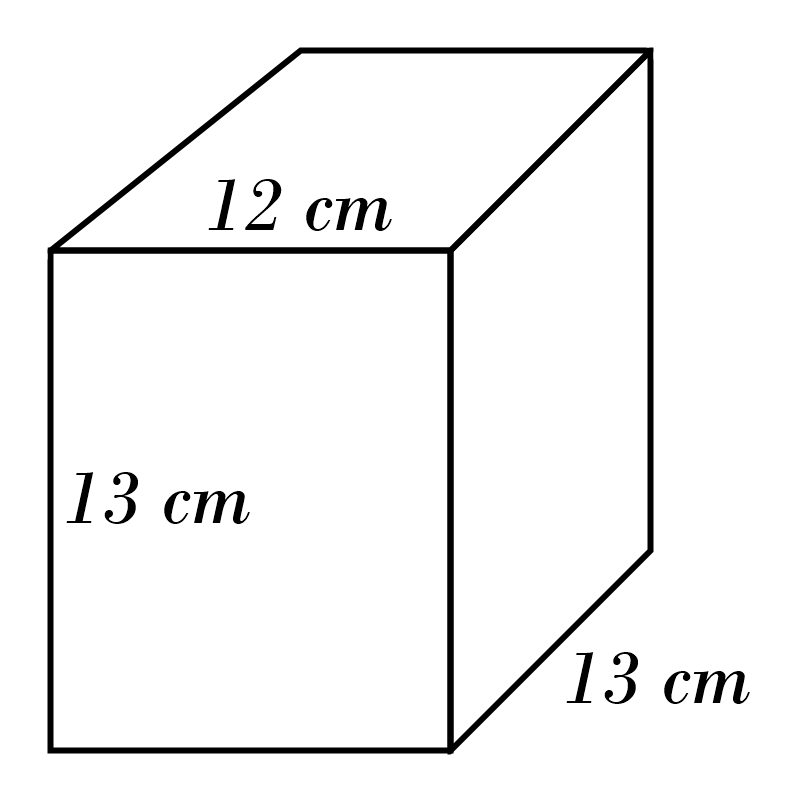
7)
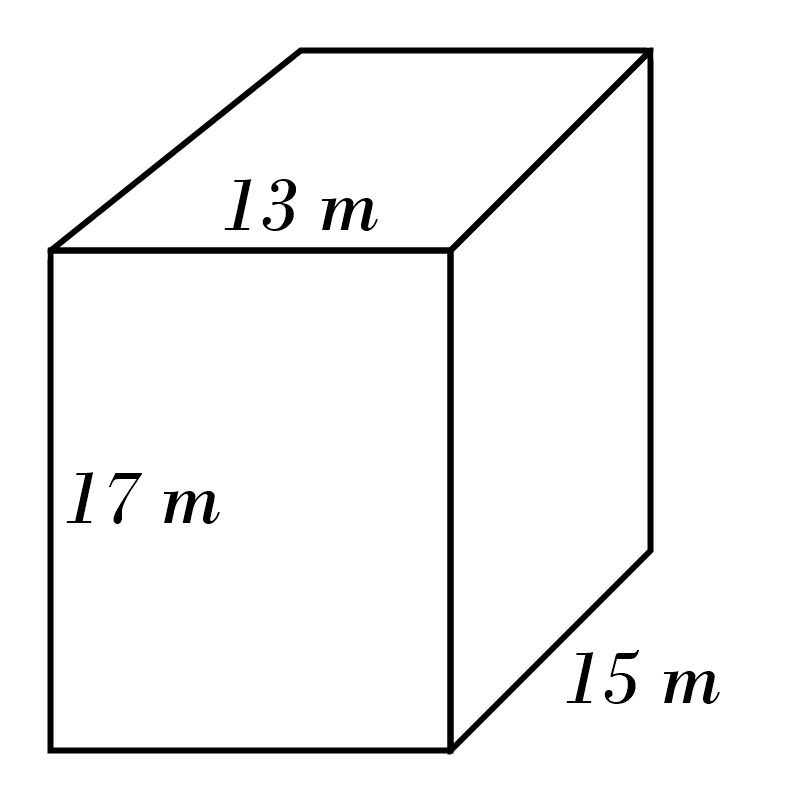
8)
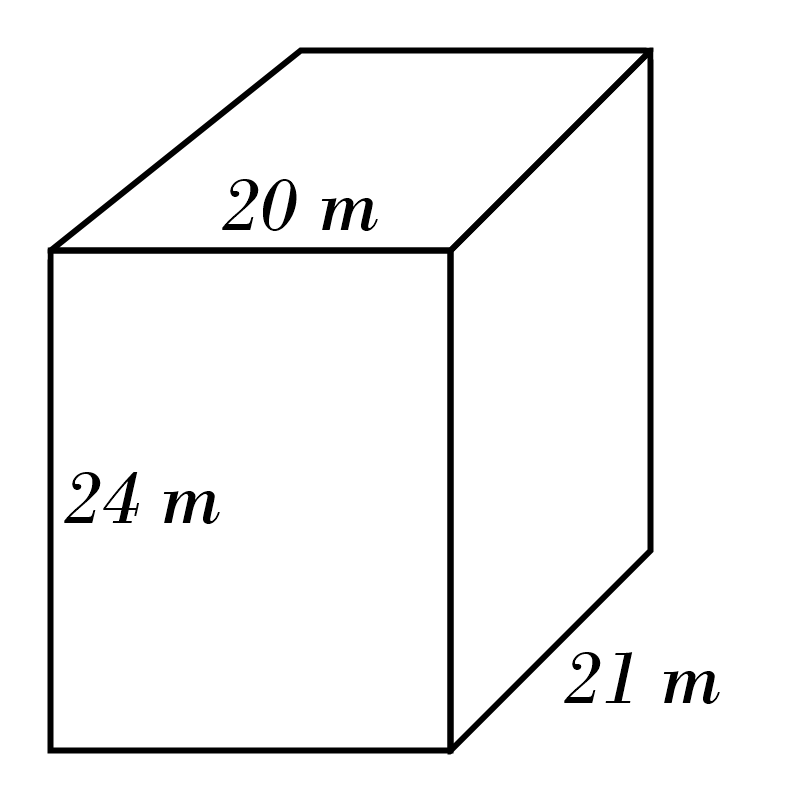
9)
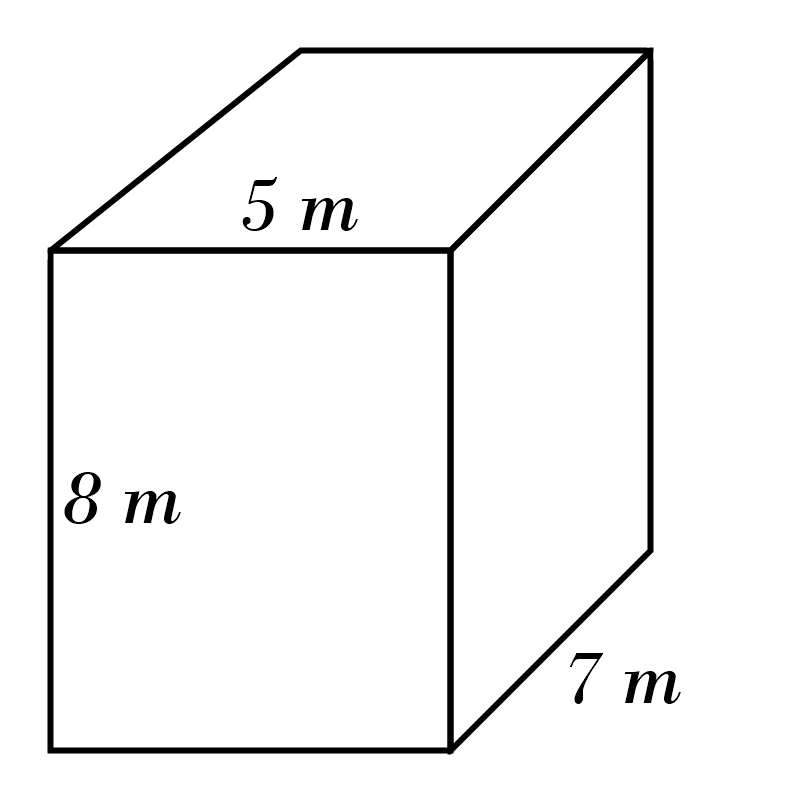
10)
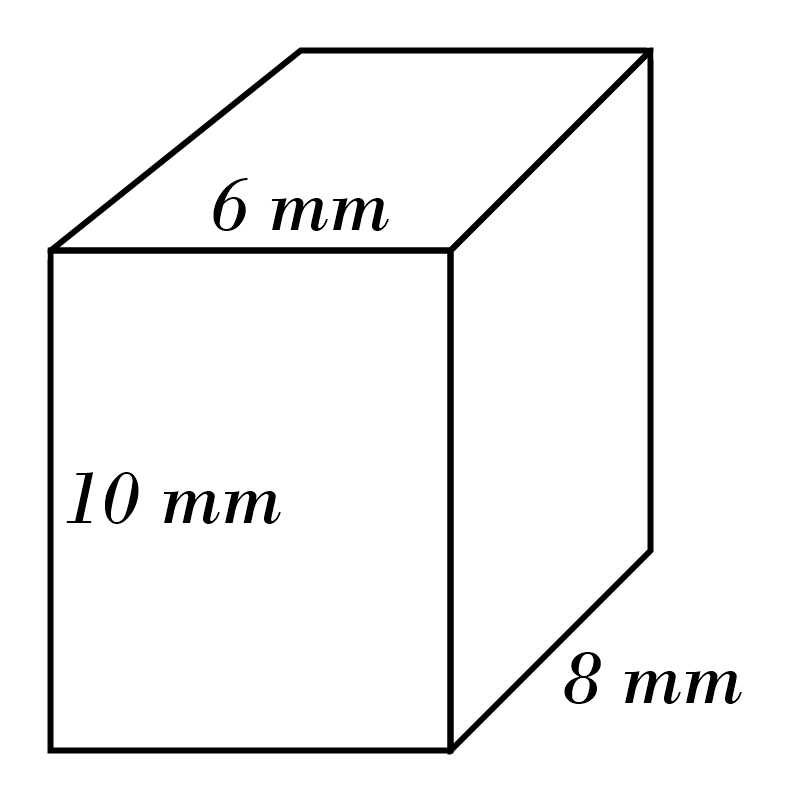
1) \(\color{red}{48} \)
m\(^3\) 
2) \(\color{red}{6840} \)
m\(^3\) 
3) \(\color{red}{1859} \)
mm\(^3\) 
4) \(\color{red}{120} \)
in\(^3\) 
5) \(\color{red}{7980} \)
in\(^3\) 
6) \(\color{red}{2028} \)
cm\(^3\) 
7) \(\color{red}{3315} \)
m\(^3\) 
8) \(\color{red}{10080} \)
m\(^3\) 
9) \(\color{red}{280} \)
m\(^3\) 
10) \(\color{red}{480} \)
mm\(^3\) 
Volume of Rectangle Prisms Practice Quiz