How to Find the Surface Area of a Cylinder
Read,4 minutes
Definition
A cylinder is a frequently seen three-dimensional solid in our environment, such as a glue stick for crafts, a soft drink that can satisfy our thirst, or a remote control battery. Taking a look at these things we see every day, we can say that a cylinder has two circular bases, one at the top and one at the bottom. These two bases are circles that look and are the same size and shape. Line segments connect these two bases, giving the cylinder its shape.
.png)
What is the Area of Surface?
The surface area is the amount of space that a three-dimensional object takes up on the outside. This idea is different from the definition of the area because the area is used to describe two-dimensional things. The surface area of a cylinder is the sum of its three parts, which are two circular bases and a side.
What does LSA stand for?
The part of a three-dimensional object that is not the base is called the lateral surface area. In a cylinder, the two bases are parallel circles joined by parts of the line that make up the cylinder's side. If you draw this part of the cylinder on a flat surface, it looks like a rectangle with a height equal to the height of the cylinder and a width equal to the sum of the circumferences of the bases.
How to Find the Area of a Cylinder's Surface
Think about a cylinder whose height is \(h\) and whose base radius is \(r\). The formula for finding a cylinder's surface area is:
\(A \ = \ 2πr^2h \ + \ 2πrh\)
The first term gives the surface area of the two bases and the second term gives the surface area of the cylinder's side. When doing this kind of evaluation, a cylinder unit's surface area must be kept in mind. The radius and the height must be given in the same unit, and the surface area will be the square of this unit. For example, if the height and radius of the bases are given in centimeters, the surface area will be given in centimeters squared.
Example:
Figure out how much it will cost to paint a right circular cylinder with a base radius of \(6\) meters and a height of \(17\) meters. If the cost of painting the container is INR \(4\) per square meter. (Take \(π \ = \ 3.14\))
Solution:
Total surface area of cylinder \(= \ 2πr \ (h \ + \ r) \ = \ 2(3.14)(6)(17 \ + \ 6) \ = \ 866.64\)m\(^2\)
The cost to paint the cylinder is \(4\) per square meter: Total cost of painting \(= \ 4 \times 866.64 \ = \ 3466.56\)
Free printable Worksheets
Exercises for Surface Area of a Cylinder
1)
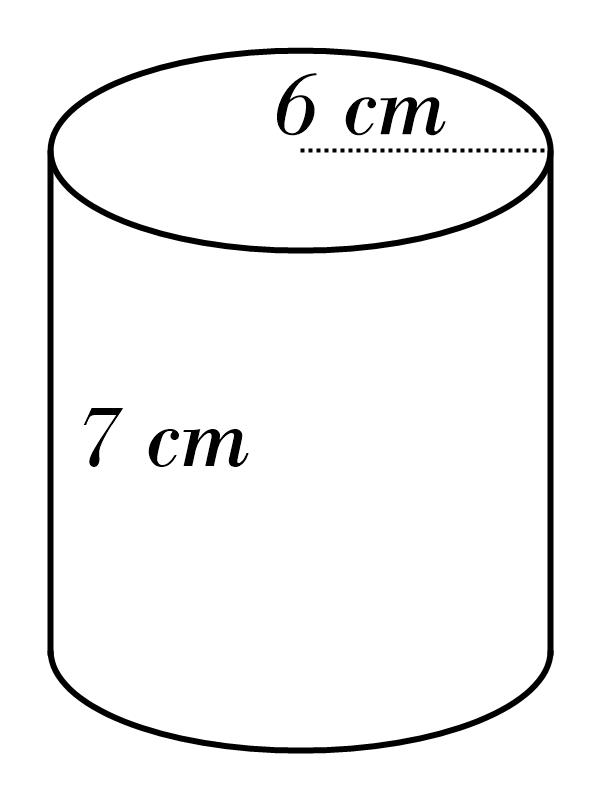
2)
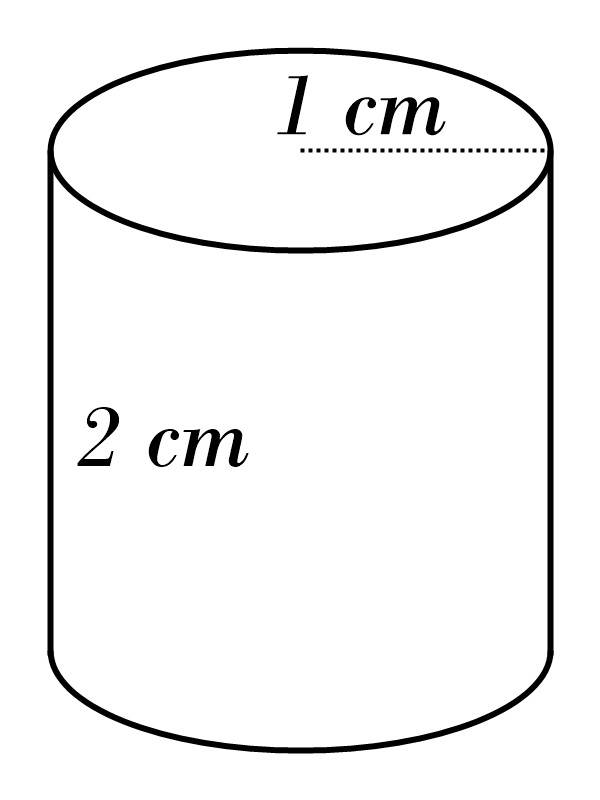
3)
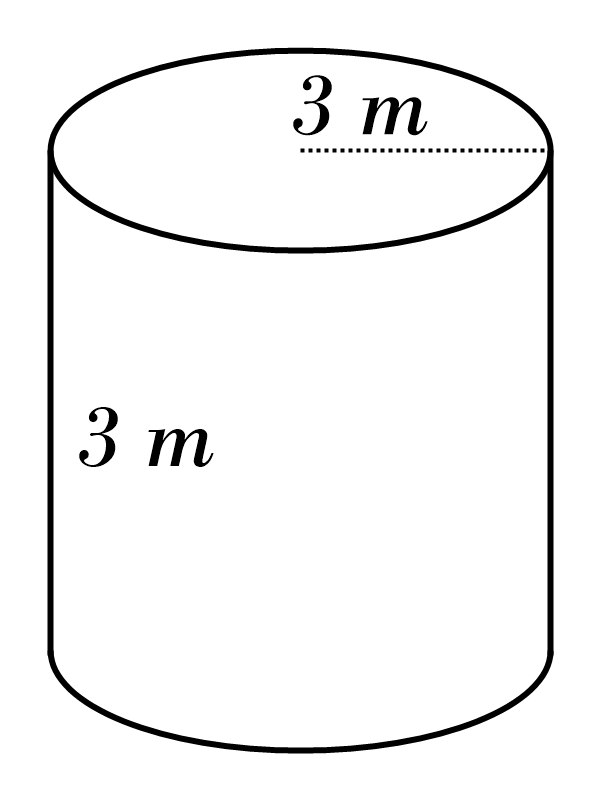
4)
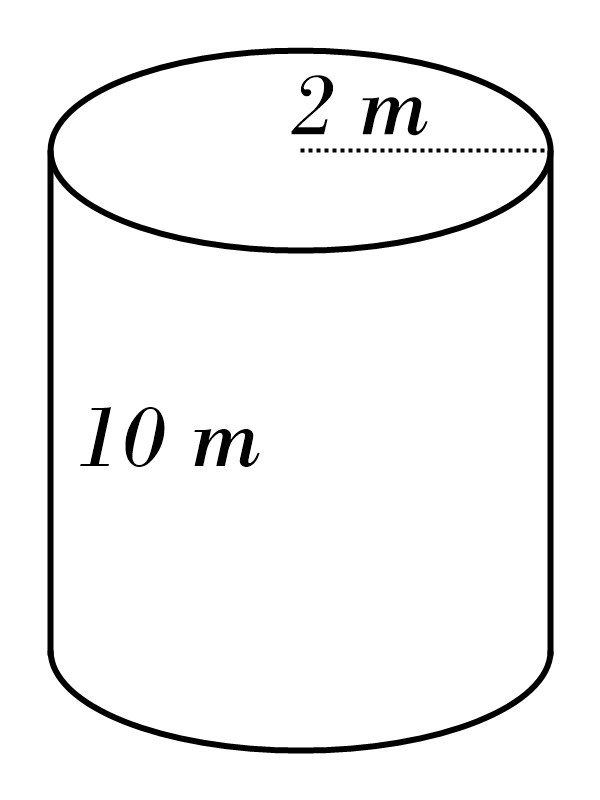
5)
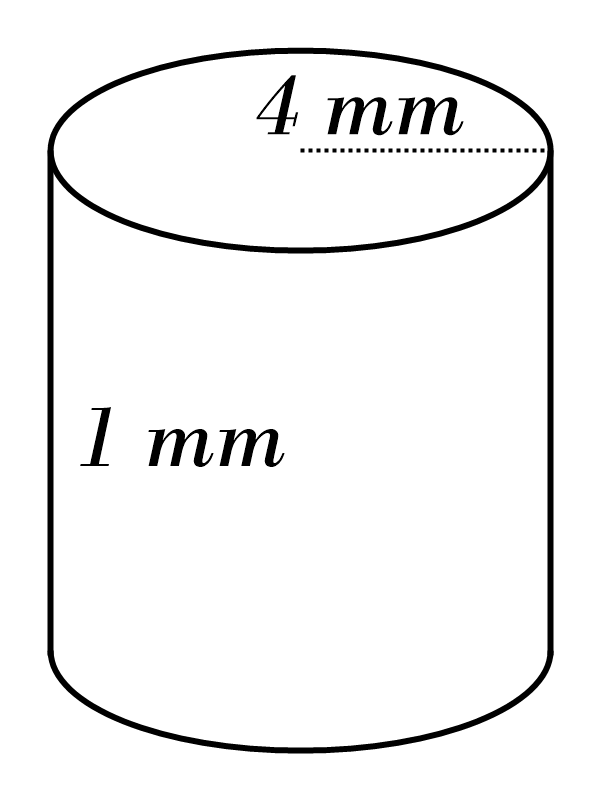
6)
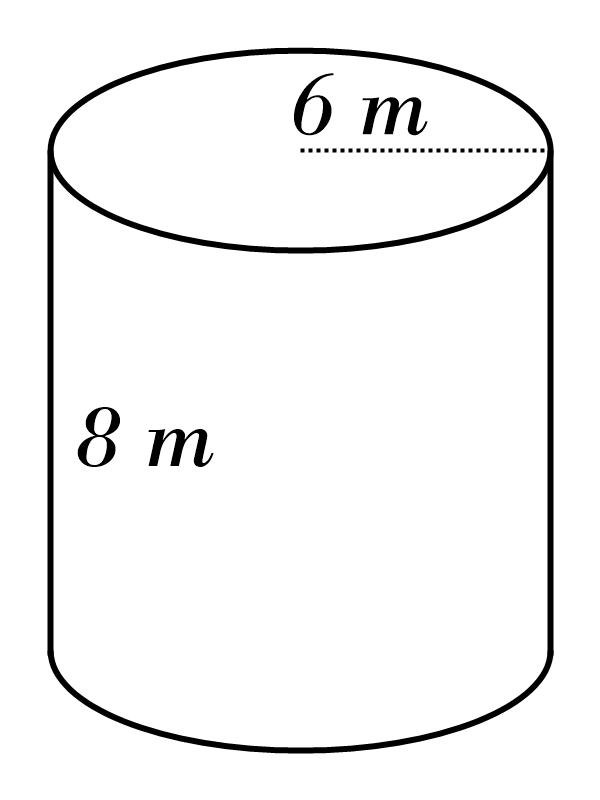
7)
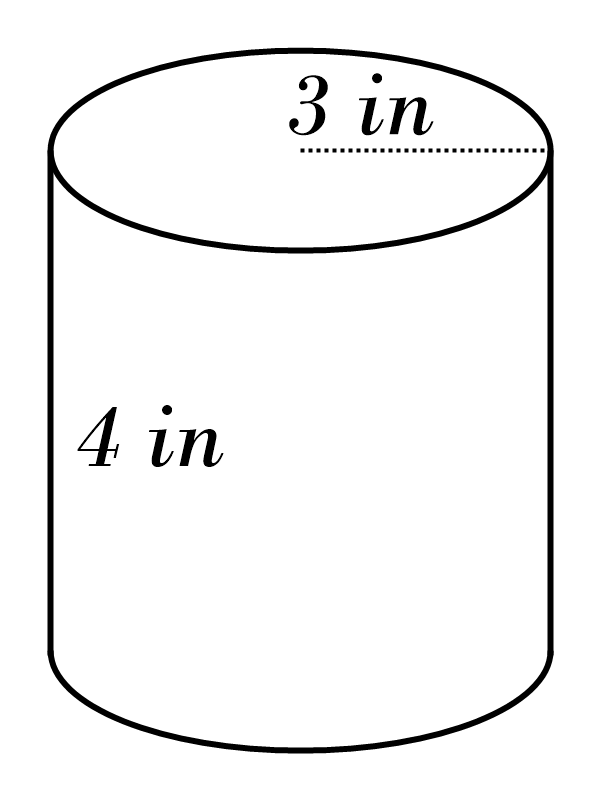
8)
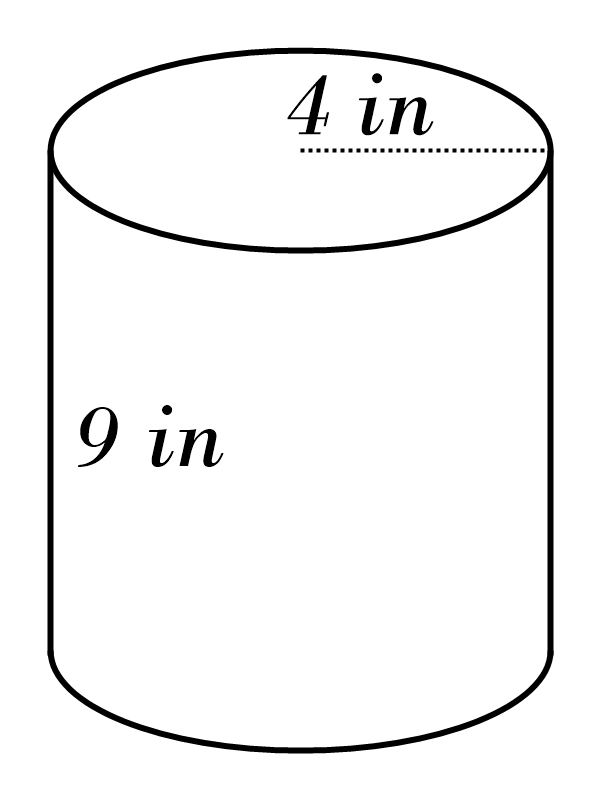
9)
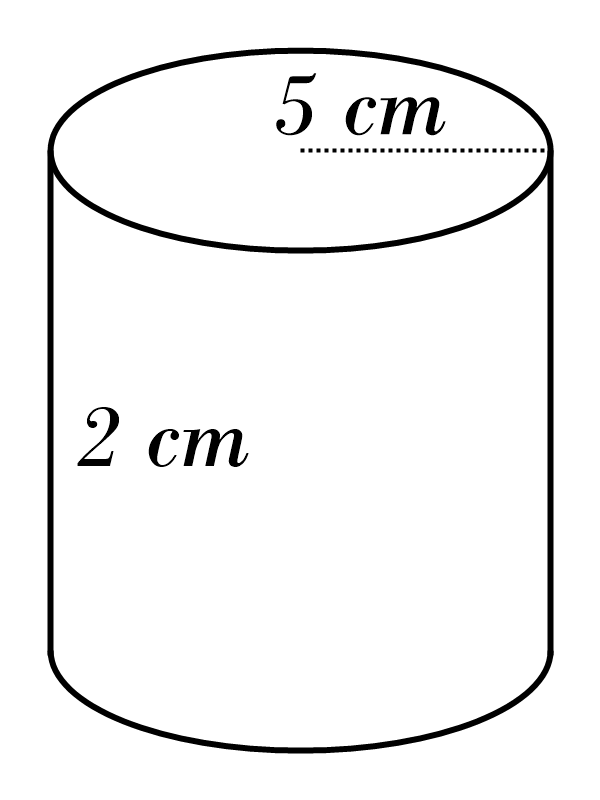
10)
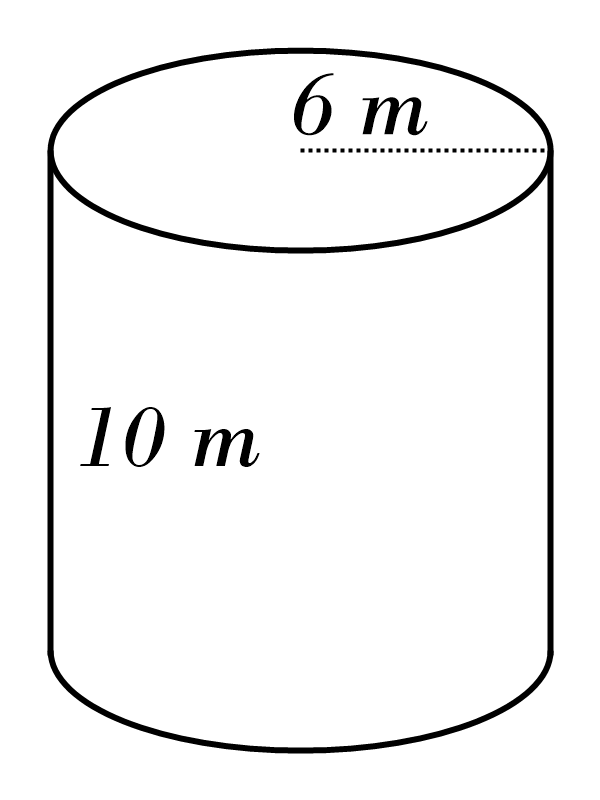
Surface Area of a Cylinder Practice Quiz